
����Ŀ����ݮ�����϶��ʢ����һ��ˮ��������ijˮ�����۵��ڲ�ݮ�������������۳ɱ�Ϊÿǧ��18Ԫ�IJ�ݮ���涨�����ڼ����۵��۲����ڳɱ����ۣ�Ҳ������ÿǧ��40Ԫ�����������֣�������y��kg�������۵���x��Ԫ/kg������һ�κ�����ϵ����ͼ��y��x�ĺ�����ϵͼ��
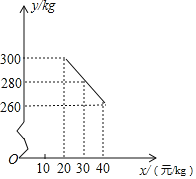
��1����y��x�ĺ�������ʽ��
��2�����ˮ�����۵�������ݮ��õ�����ΪWԪ����W�����ֵ��
���𰸡���1��y����2x+340��18��x��40������2����x��40ʱ��Wȡ�����ֵ�����ֵΪ5720.
��������
��1����y��kx+b��Ȼ�����ô���ϵ�������һ�κ����Ľ���ʽ���ɣ�
��2�����ݡ�������=ÿǧ�������ǧ�������������W��x�ĺ�����ϵʽ��Ȼ�����ö��κ�������ֵ���ɣ�
�⣺��1����y��kx+b��
��x��20��y��300��x��30��y��280���룬�ã�
![]() ��
��
��ã�![]() ��
��
��y����2x+340��18��x��40����
��2���������⣬�ã�W����x��18������2x+340��
����2x2+376x��6120
����2��x��94��2+11552��
��a����2��0��
�൱x��94ʱ��W��x�����������
����18��x��40�У���x��40ʱ��Wȡ�����ֵ�����ֵΪ5720��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ƹ����������ͳ��ĿУ��Ϊ��һ���ƶ�����Ŀ�ķ�չ.ѧУ����������Ʒ�깺��ס��������ͺ�ƹ�������ɸ�����֪3������ƹ�����5������ƹ������50Ԫ��2������ƹ�����3������ƹ������31Ԫ.
��1����1������ƹ�����1������ƹ������ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵ�ƹ����200����Ҫ�����ƹ�������������������ƹ�����������3��������Ƴ���ʡǮ�Ĺ�������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ�����ݵ��������������飬���±���
��ȡ������ | 40 | 100 | 150 | 500 | 1000 | 1500 |
�ŵ�Ʒ�� | 36 | 92 | 145 | 474 | 950 | 1427 |
�ŵ�ƷƵ�� |
��1��������е��ŵ�Ʒ��Ƶ�ʣ���ȷ��0.001��
��2�����ݳ�˵ĵ����ŵ�Ʒ��Ƶ�ʣ��������������ŵ�Ʒ�ĸ��ʣ���ȷ��0.01��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
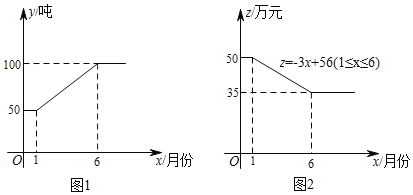
����Ŀ�����ż����ķ�չ������ij��˾2018����õ�����ԭ��������Ʒ����������ԭ�ϵ�����y���֣����·�x֮��Ĺ�ϵ��ͼ1��ʾ��ÿ������ԭ���������IJ�Ʒ���ۼ�z����Ԫ�����·�x֮��Ĺ�ϵ��ͼ2��ʾ����֪��ÿ����������ԭ�ϼӹ��ɵIJ�Ʒ�ijɱ�Ϊ20��Ԫ��
��1������ù�˾��������ԭ�ϵ�����y���֣����·�x֮��ĺ�����ϵʽ��
��2�����ù�˾��������ԭ���������IJ�Ʒ���¶�ȫ�����ۣ����ĸ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����Բ
����Բ![]() ��ֱ��
��ֱ��![]() ����
����![]() ���
���![]() �غϣ���Բ
�غϣ���Բ![]() ��
��![]() ���ٶȴ��������ƶ������˶������У���
���ٶȴ��������ƶ������˶������У���![]() ��
��![]() ʼ����
ʼ����![]() ���ڵ�ֱ���ϣ����˶�ʱ��Ϊ
���ڵ�ֱ���ϣ����˶�ʱ��Ϊ![]() ����Բ
����Բ![]() ��
��![]() ���ص����ֵ����Ϊ
���ص����ֵ����Ϊ![]() ��
��
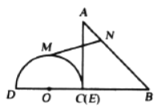
��1����![]() ʱ�����
ʱ�����![]() �ǰ�Բ
�ǰ�Բ![]() ��һ�㣬��
��һ�㣬��![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() �����ֵΪ_________��
�����ֵΪ_________��![]() ����СֵΪ________��
����СֵΪ________��
��2����ƽ�ƹ����У�����![]() ��
��![]() ���е��غ�ʱ�����Բ
���е��غ�ʱ�����Բ![]() ��
��![]() �ص����ֵ����
�ص����ֵ����![]() ��
��
��3����![]() Ϊ��ֵʱ����Բ
Ϊ��ֵʱ����Բ![]() ��
��![]() �ı����ڵ�ֱ�����У�
�ı����ڵ�ֱ�����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
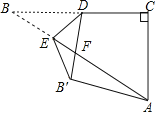
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬BC��2![]() ��AC��2����D��BC���е㣬��E�DZ�AB��һ���㣬��DE����ֱ�߰ѡ�BDE���۵���B��DE��λ�ã�B��D��AB�ڵ�F������AB��FΪֱ�������Σ���AE�ij�Ϊ_____��
��AC��2����D��BC���е㣬��E�DZ�AB��һ���㣬��DE����ֱ�߰ѡ�BDE���۵���B��DE��λ�ã�B��D��AB�ڵ�F������AB��FΪֱ�������Σ���AE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
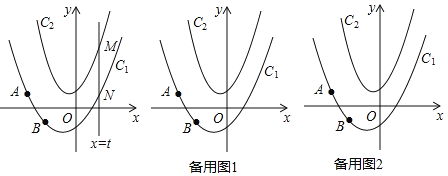
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������C1��y��ax2+bx��1������A����2��1���͵�B����1����1����������C2��y��2x2+x+1����ֱ��x��t��������C1���ڵ�N����������C2���ڵ�M��
��1����������C1�ı���ʽ��
��2������AMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����t��ֵ��
��3���ڣ�2���������£���������C1��y�ύ�ڵ�P����M��y���Ҳ��������C2�ϣ�����AM��y���ڵ�K������KN����ƽ������һ��Q������KQ��QN����KQ��1�ҡ�KNQ����BNPʱ����ֱ��д����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
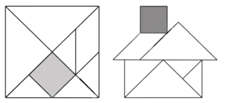
����Ŀ�������ɰ塱���������ȵ�һ��Խ���죬����ƴ��������Ȥ��ͼ�Σ�����Ϊ������ħ�塱��ͼ�����ɱ߳�![]() �������α���ֳ�7�������ɵġ����ɰ塱ͼ�����øá����ɰ塱ƴ�ɵ�һ�����ҡ���ͼ�Σ��á����ɰ塱��7��ͼ��֮һ�������α߳�Ϊ_______
�������α���ֳ�7�������ɵġ����ɰ塱ͼ�����øá����ɰ塱ƴ�ɵ�һ�����ҡ���ͼ�Σ��á����ɰ塱��7��ͼ��֮һ�������α߳�Ϊ_______![]() (�����������).
(�����������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Сܿ��Ƶġ���Բ��һ������֪Բ�����ߡ��ij߹���ͼ���̣�
��֪����O ����O ��һ�� P��
��������O ��һ�����ߣ�ʹ�������߾����� P��
������������ OP���� OP �Ĵ�ֱƽ���� l���� OP �ڵ� A��
���� A ΪԲ�ģ�AO Ϊ�뾶��Բ������O �ڵ� M��
����ֱ�� PM����ֱ�� PM ��Ϊ��O �����ߣ�

����Сܿ��Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�(������ͼ�ۼ�)
��2����������֤����
֤�������� OM��
����ͼ��֪��A Ϊ OP �е㣬
��OP Ϊ��A ֱ����
��� ��90�㣨 ���������������ݣ�
�� OM��PM��
�֡ߵ� M �ڡ�O �ϣ�
��PM �ǡ�O �����ߣ��� ���������������ݣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com