
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 的直径
的直径![]() .点
.点![]() 与点
与点![]() 重合,半圆
重合,半圆![]() 以
以![]() 的速度从左向右移动,在运动过程中,点
的速度从左向右移动,在运动过程中,点![]() 、
、![]() 始终在
始终在![]() 所在的直线上.设运动时间为
所在的直线上.设运动时间为![]() ,半圆
,半圆![]() 与
与![]() 的重叠部分的面积为
的重叠部分的面积为![]() .
.
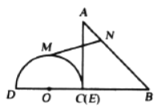
(1)当![]() 时,设点
时,设点![]() 是半圆
是半圆![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,则
上一点,则![]() 的最大值为_________;
的最大值为_________;![]() 的最小值为________.
的最小值为________.
(2)在平移过程中,当点![]() 与
与![]() 的中点重合时,求半圆
的中点重合时,求半圆![]() 与
与![]() 重叠部分的面积
重叠部分的面积![]() ;
;
(3)当![]() 为何值时,半圆
为何值时,半圆![]() 与
与![]() 的边所在的直线相切?
的边所在的直线相切?
【答案】(1)24cm,![]() cm;(2)
cm;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)当![]() 与点
与点![]() 重合,点
重合,点![]() 与点
与点![]() 重合时,
重合时,![]() 最大,此时
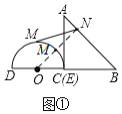
最大,此时![]() 如图①,过点
如图①,过点![]() 作
作![]() 于
于![]() ,与半圆交于点
,与半圆交于点![]() ,此时
,此时![]() 最小,
最小,![]() ,
,
![]() ,所以
,所以![]() ;
;
(2)当点![]() 与
与![]() 的中点重合时,如图②,点
的中点重合时,如图②,点![]() 移动了
移动了![]() ,设半圆与
,设半圆与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,
,![]() ;
;
(3)当半圆![]() 与直线
与直线![]() 相切时,运动的距离为0或12,所以
相切时,运动的距离为0或12,所以![]() (秒
(秒![]() 或6(秒
或6(秒![]() ;当半圆
;当半圆![]() 与直线
与直线![]() 相切时,如图③,连接
相切时,如图③,连接![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,移动的距离为
,移动的距离为![]() ,运动时间为
,运动时间为![]() (秒
(秒![]() .
.
解:解(1)当![]() 与点
与点![]() 重合,点
重合,点![]() 与点
与点![]() 重合时,
重合时,![]() 最大,此时
最大,此时![]()
如图①,过点![]() 作
作![]() 于
于![]() ,与半圆交于点
,与半圆交于点![]() ,此时
,此时![]() 最小,
最小,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]() ,
,
故答案为![]() ,
,![]() ;
;
(2)当点![]() 与
与![]() 的中点重合时,如图②,点
的中点重合时,如图②,点![]() 移动了
移动了![]() ,
,
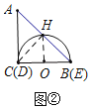
设半圆与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() .
.
![]() 为直径,
为直径,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)当半圆![]() 与直线
与直线![]() 相切时,运动的距离为0或12,
相切时,运动的距离为0或12,
![]() (秒
(秒![]() 或6(秒
或6(秒![]() ;
;
当半圆![]() 与直线
与直线![]() 相切时,如图③,
相切时,如图③,
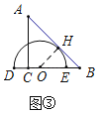
连接![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
移动的距离为![]() ,
,
运动时间为![]() (秒
(秒![]() ,
,
综上所述,当![]() 为0或6或
为0或6或![]() 时,半圆
时,半圆![]() 与
与![]() 的边所在的直线相切.
的边所在的直线相切.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
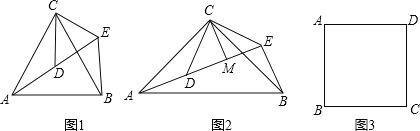
【题目】![]() 问题发现
问题发现
如图![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在同一直线上,连接BE.
在同一直线上,连接BE.
填空:
![]() 的度数为______;
的度数为______;
![]() 线段
线段![]() 之间的数量关系为______.
之间的数量关系为______.
![]() 拓展探究
拓展探究
如图![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() 在同一直线上,CM为
在同一直线上,CM为![]() 中DE边上的高,连接BE,请判断
中DE边上的高,连接BE,请判断![]() 的度数及线段
的度数及线段![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
![]() 解决问题
解决问题
如图3,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点A到BP的距离.
,请直接写出点A到BP的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建设工程队计划每小时挖掘土石方![]() 方,现决定租用甲、乙两种型号的挖掘机来完成这项工作,已知一台甲型挖掘机与一台乙型挖掘机每小时共挖土
方,现决定租用甲、乙两种型号的挖掘机来完成这项工作,已知一台甲型挖掘机与一台乙型挖掘机每小时共挖土![]() 方,
方,![]() 台甲型挖掘机与
台甲型挖掘机与![]() 台乙型挖掘机恰好能完成每小时的挖掘量.
台乙型挖掘机恰好能完成每小时的挖掘量.
(1)求甲、乙两种型号的挖掘机每小时各挖土多少方?
(2)若租用一台甲型挖掘机每小时![]() 元,租用一台乙型挖掘机每小时
元,租用一台乙型挖掘机每小时![]() 元,且每小时支付的总租金不超过
元,且每小时支付的总租金不超过![]() 元,又恰好完成每小时的挖掘量,请设计该工程队的租用方案.
元,又恰好完成每小时的挖掘量,请设计该工程队的租用方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,求作
,求作![]() 的外心
的外心![]() ,以下是甲、乙两同学的作法:对于两人的作法:
,以下是甲、乙两同学的作法:对于两人的作法:
甲:如图1,(1)作![]() 的垂直平分线
的垂直平分线![]() ;
;
(2)作![]() 的垂直平分线
的垂直平分线![]() ;
;
(3)![]() ,
,![]() 交于点
交于点![]() ,则点
,则点![]() 即为所求.
即为所求.
乙:如图2,(1)作![]() 的平分线
的平分线![]() ;
;
(2)作![]() 的垂直平分线
的垂直平分线![]() ;
;
(3)![]() ,
,![]() 交于点
交于点![]() ,则点
,则点![]() 即为所求.
即为所求.
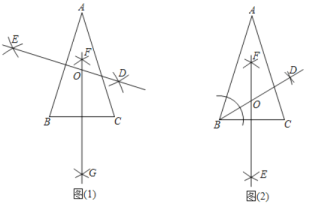
对于两人的作法,正确的是( )
A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象.
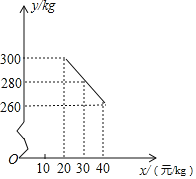
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小花在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小花身高1.5米,当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,二次函数![]() 的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:
的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:![]() 交BD于点E,连接BC的直线交直线l于K点.
交BD于点E,连接BC的直线交直线l于K点.
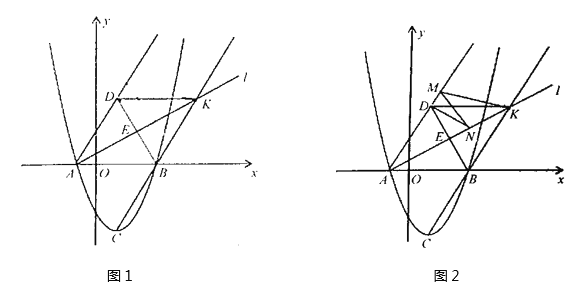
(1)问:在四边形ABKD内部是否存在点P,使它到四边形ABKD四边的距离都相等?
若存在,请求出点P的坐标;若不存在,请说明理由;
(2)若M,N分别为直线AD和直线l上的两个动点,连结DN,NM,MK,如图2,求DN+NM+MK和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com