
【题目】如图1,在平面直角坐标系xoy中,二次函数![]() 的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:
的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:![]() 交BD于点E,连接BC的直线交直线l于K点.
交BD于点E,连接BC的直线交直线l于K点.
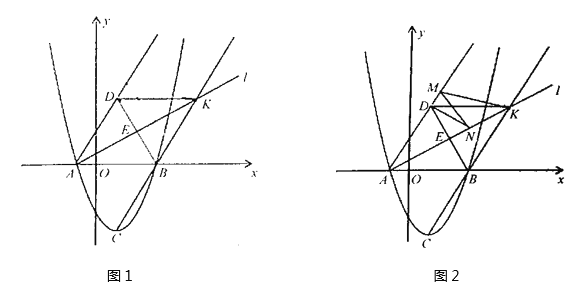
(1)问:在四边形ABKD内部是否存在点P,使它到四边形ABKD四边的距离都相等?
若存在,请求出点P的坐标;若不存在,请说明理由;
(2)若M,N分别为直线AD和直线l上的两个动点,连结DN,NM,MK,如图2,求DN+NM+MK和的最小值.
【答案】(1) 四边形ABCD内部存在点P(2,![]() )到四边形ABCD四边的距离相等;(2)8.
)到四边形ABCD四边的距离相等;(2)8.
【解析】
(1)由抛物线解析式求点A、B、C、D的坐标,求直线BC解析式,把直线BC与直线l的解析式联立方程组,求得的解为点K坐标,因此求得AB=BK=KD=AD=4,即四边形ABKD为菱形.由菱形性质可知对角线平分一组对角,故对角线AK、BD交点E在菱形四个内角的平分线上,所以点E到四边距离相等,即为符合题意的点P.
(2)由菱形性质可知点B、D关于直线AK对称,故有DN=BN,所以当点B、N、M在同一直线上时,DN+MN=BN+MN=BM最小.作点K关于直线AD对称点Q,得MK=MQ,所以当点Q、M、B在同一直线上时,BM+MK=BM+MQ=BQ最小,即BQ的长为DN+NM+MK的最小值.由AK平分∠DAB可求得点K到直线AD距离等于点K的纵坐标,进而求得KQ的长;再由BK∥AD得∠BKQ=∠DRQ=90°,利用勾股定理即求得BQ的长.
(1)在四边形ABKD内部存在点P到四边形ABKD四边的距离都相等.
当y=0时,![]()
解得:x1=-1,x2=3
∴A(-1,0),B(3,0),AB=4
∵![]()
∴顶点C(1,-2![]() )
)
∵点D为点C关于x轴的对称点
∴D(1,2![]() ),
),![]()
设直线BC解析式为y=bx+c
∴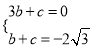 , 解得:
, 解得: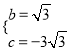
∴直线BC:![]()
∵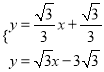 ,解得:
,解得:
∴K(5,2![]() )
)
∴![]() ,DK∥x轴,DK=5-1=4
,DK∥x轴,DK=5-1=4
∴AB=BK=DK=AD=4
∴四边形ABKD是菱形
∴对角线AK、BD平分一组对角,
∴AK、BD交点E(1,![]() )到菱形四边距离相等
)到菱形四边距离相等
∴点P与点E重合时,即符合题意的点
∴在四边形ABKD内部存在点P(1,![]() )到四边形ABKD四边的距离都相等.
)到四边形ABKD四边的距离都相等.
(2)过点K作KF⊥x轴于点F,作点K关于直线AD的对称点Q,KQ与直线AD相交于点R,连接MQ、QB、NB
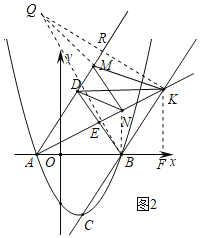
∵菱形ABKD中,AK与BD互相垂直平分
∴点B、D关于直线AK对称
∴DN=BN
∴当点B、N、M在同一直线上时,DN+NM=BN+NM=BM最小
∵点K、Q关于直线AD对称
∴KQ⊥AD,QR=KR,MK=MQ
∴当点Q、M、B在同一直线上时,BM+MK=BM+MQ=BQ最小
∴BQ的长为DN+NM+MK的最小值
∵AK平分∠DAB,KF⊥AB,KR⊥AD,yK=2![]()
∴KF=KR=2![]()
∴KQ=2KR=4![]()
∵BK∥AD
∴∠BKQ=∠DRQ=90°
∴Rt△BKQ中,BQ=![]()
∴DN+NM+MK和的最小值为8.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 的直径
的直径![]() .点
.点![]() 与点
与点![]() 重合,半圆
重合,半圆![]() 以
以![]() 的速度从左向右移动,在运动过程中,点
的速度从左向右移动,在运动过程中,点![]() 、
、![]() 始终在
始终在![]() 所在的直线上.设运动时间为
所在的直线上.设运动时间为![]() ,半圆
,半圆![]() 与
与![]() 的重叠部分的面积为
的重叠部分的面积为![]() .
.
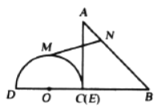
(1)当![]() 时,设点
时,设点![]() 是半圆
是半圆![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,则
上一点,则![]() 的最大值为_________;
的最大值为_________;![]() 的最小值为________.
的最小值为________.
(2)在平移过程中,当点![]() 与
与![]() 的中点重合时,求半圆
的中点重合时,求半圆![]() 与
与![]() 重叠部分的面积
重叠部分的面积![]() ;
;
(3)当![]() 为何值时,半圆
为何值时,半圆![]() 与
与![]() 的边所在的直线相切?
的边所在的直线相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段 AB 先向右平移 5 个单位,再将所得线段绕原点按顺时针方向旋转 90°,得到线段 AB ,则点 B 的对应点 B′的坐标是( )
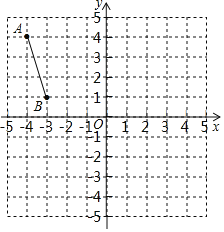
A.(-4 , 1)B.( -1, 2)C.(4 ,- 1)D.(1 ,- 2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,DB⊥MN于点B.
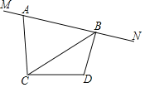
(1)如图,求证:BD+AB=![]() BC;
BC;
(2)直线MN绕点A旋转,在旋转过程中,当∠BCD=30°,BD=![]() 时,求BC的值.
时,求BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
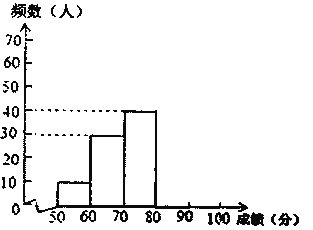
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
已知:⊙O 及⊙O 外一点 P.
求作:⊙O 的一条切线,使这条切线经过点 P.
作法:①连接 OP,作 OP 的垂直平分线 l,交 OP 于点 A;
②以 A 为圆心,AO 为半径作圆,交⊙O 于点 M;
③作直线 PM,则直线 PM 即为⊙O 的切线.

根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接 OM,
由作图可知,A 为 OP 中点,
∴OP 为⊙A 直径,
∴∠ =90°( )(填推理的依据)
即 OM⊥PM.
又∵点 M 在⊙O 上,
∴PM 是⊙O 的切线.( )(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
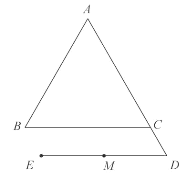
【题目】如图,在等边![]() 中,D为边AC的延长线上一点(
中,D为边AC的延长线上一点(![]() ),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)连接DF并延长交AB于点H,用等式表示线段AH与CG的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (
(![]() 为常数,
为常数,![]() )的图象过点
)的图象过点![]() 和点
和点![]() ,函数图象最低点
,函数图象最低点![]() 的纵坐标为
的纵坐标为![]() .直线
.直线![]() 的解析式为
的解析式为![]()
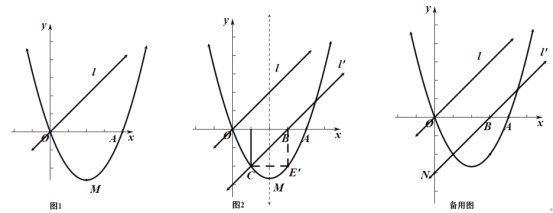
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 直线
直线![]() 沿
沿![]() 轴向右平移,得直线
轴向右平移,得直线![]() ,
,![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与
,与![]() 轴下方的抛物线相交于点
轴下方的抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,把
,把![]() 沿直线
沿直线![]() 折叠,当点
折叠,当点![]() 恰好落在抛物线上点
恰好落在抛物线上点![]() 时(图
时(图![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,
的条件下,![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,P为
,P为![]() 上的动点,当
上的动点,当![]() 为等腰三角形时,求符合条件的点
为等腰三角形时,求符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com