
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,DB⊥MN于点B.
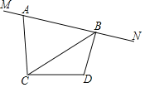
(1)如图,求证:BD+AB=![]() BC;
BC;
(2)直线MN绕点A旋转,在旋转过程中,当∠BCD=30°,BD=![]() 时,求BC的值.
时,求BC的值.
【答案】(1)证明见解析;(2)BC=![]() +1或
+1或![]() ﹣1.
﹣1.
【解析】
(1)过点C作CE⊥CB于点C,与MN交于点E,易证:∠BCD=∠ACE,∠CBD=∠CEA,进而证明△ACE≌△DCB(AAS),可得:△ECB为等腰直角三角形,即:BE=![]() CB,进而得到结论;
CB,进而得到结论;
(2)分两种情况讨论:①当C,D在直线MN的同侧时,②当C,D在直线MN的异侧时,分别求出BC的值,即可.
(1)过点C作CE⊥CB于点C,与MN交于点E,如图1,
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE,
∵DB⊥MN,
∴∠ABC+∠CBD=90°,
∵CE⊥CB
∴∠ABC+∠CEA=90°,
∴∠CBD=∠CEA.
又∵AC=DC,
∴△ACE≌△DCB(AAS),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=![]() CB.
CB.
又∵BE=AE+AB,
∴BE=BD+AB,
∴BD+AB=![]() CB.
CB.
(2)①当C,D在直线MN的同侧时,连接AD,过点D作DF⊥BC于点F,如图2,
∵AC=CD,∠ACD=90°,
∴∠CAD=∠ADC=45°,
∵∠ACD=∠ABD=90°,
∴点A,点C,点D,点B四点共圆,
∴∠CAD=∠CBD=45°,且DF⊥BC,
∴∠FBD=∠FDB=45°,且BD=![]() ,
,
∴BF=DF=1,
∵∠BCD=30°,DF⊥BC,
∴CF=![]() DF=
DF=![]() ,
,
∴BC=CF+BF=![]() +1,
+1,
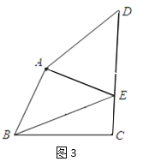
②当C,D在直线MN的异侧时,连接AD,过点D作DF⊥BC于点F,如图3,
∵AC=CD,∠ACD=90°,
∴∠CAD=∠ADC=45°,
∵∠ACD=∠ABD=90°,
∴点A,点C,点D,点B四点共圆,
∴∠CAD=∠DBF=45°,且DF⊥BC,
∴∠FBD=∠FDB=45°,且BD=![]() ,
,
∴BF=DF=1,
∵∠BCD=30°,DF⊥BC,
∴CF=![]() DF=
DF=![]() ,
,
∴BC=CF﹣BF=![]() ﹣1.
﹣1.
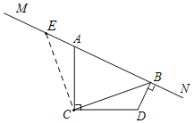
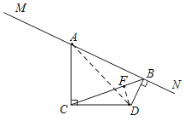
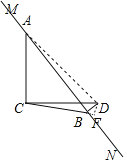
图1 图2 图3


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=x2+2kx+k﹣1(k为常数),下列说法正确的个数是( )
(1)对任意实数k,函数与x轴有两个交点
(2)当x≥﹣k时,函数y的值都随x的增大而增大
(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上
(4)对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发两小时,甲车到达B地后立即调头,并保持原速度与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(干米),甲车行驶的时间为x小时,y与x之间的函数图象如图所示,则当甲车重返A地时,乙车距离C地________千米.
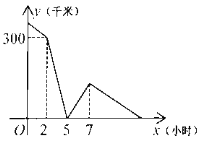
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,二次函数![]() 的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:
的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:![]() 交BD于点E,连接BC的直线交直线l于K点.
交BD于点E,连接BC的直线交直线l于K点.
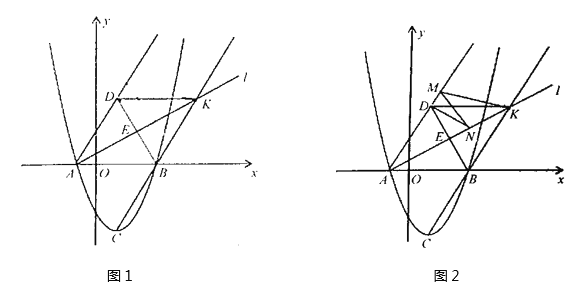
(1)问:在四边形ABKD内部是否存在点P,使它到四边形ABKD四边的距离都相等?
若存在,请求出点P的坐标;若不存在,请说明理由;
(2)若M,N分别为直线AD和直线l上的两个动点,连结DN,NM,MK,如图2,求DN+NM+MK和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年郑州市城镇民营企业就业人数突破20万,为了解城镇民营企业员工每月的收入状况,统计局对全市城镇企业民营员工2014年月平均收入随机抽样调查,将抽样的数据按“2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上”分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.
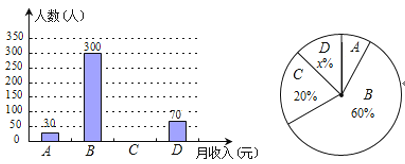
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有_____人,在扇形统计图中x的值为_____,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是_____;
(2)将不完整的条形图补充完整,并估计我市2013年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约多少人?
(3)统计局根据抽样数据计算得到,2013年我市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上一动点,以点
边上一动点,以点![]() 为顶点,
为顶点,![]() 为一腰作等腰
为一腰作等腰![]() ,使
,使![]() ,且
,且![]() ,设
,设![]() ,
,![]() ,我们称
,我们称![]() 为
为![]() 的“顶补三角形”.
的“顶补三角形”.
(1)求![]() 与
与![]() 的数量关系;
的数量关系;
(2)如图2,![]() 为
为![]() 的“顶补三角形”,过点
的“顶补三角形”,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点
于点![]() ,若四边形
,若四边形![]() 是平行四边形,求证:
是平行四边形,求证:![]() ;
;
(3)如图3,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() B,
B,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.
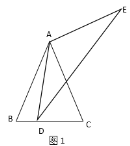

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com