
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
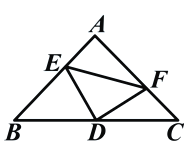
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个矩形的两邻边之比为 ![]() ,则称该矩形为“特比矩形”.
,则称该矩形为“特比矩形”.
(1)如图①,在“特比矩形”ABCD中, ![]() =
= ![]() ,求∠AOD的度数;
,求∠AOD的度数; 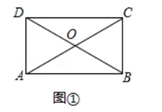
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB= ![]() ,求矩形CDEF的面积;
,求矩形CDEF的面积; 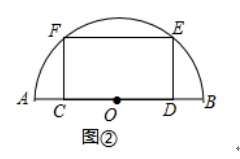
(3)在平面直角坐标系xOy中,⊙O的半径为 ![]() ,点Q的坐标为(q,2
,点Q的坐标为(q,2 ![]() ),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )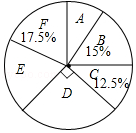
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
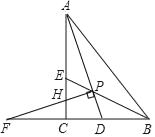
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习过程中遇到这样一个问题:
“一个木箱漂浮在河水中,随河水向下游漂去,在木箱上游和木箱下游各有一条小船,分别为甲船和乙船,两船距木箱距离相等,同时划向木箱,若两船在静水中划行的速度是30m/min,那么哪条小船先遇到木箱?”
小明是这样分析解决的:
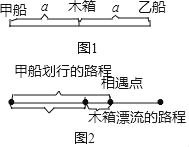
小明想通过比较甲乙两船遇见木箱的时间,知道哪条小船先遇见木箱.设甲船遇见木箱的时间为xmin,乙船遇见木箱的时间为ymin,开始时两船与木箱距离相等,都设为am,如图1.
如图2,利用甲船划行的路程﹣木箱漂流的路程=开始时甲船与木箱的距离:
列方程:x(30+5)﹣5x=a
解得,x=![]()
所以甲船遇见木箱的时间为![]() min.
min.
(1)参照小明的解题思路继续完成上述问题;
(2)借鉴小明解决问题的方法和(1)中发现的结论解决下面问题:
问题:“在一河流中甲乙两条小船,同时从A地出发,甲船逆流而上,乙船顺流而下;划行10分钟后,乙船发现船上木箱不知何时掉入水中,乙船立即通知甲船,两船同时掉头寻找木箱,若两船在静水中划行的速度是v(单位:m/min,v大于5),水流速度是5m/min,两船同时遇见木箱,那么木箱是出发几分钟后掉入水中的?”
查看答案和解析>>
科目:初中数学 来源: 题型:
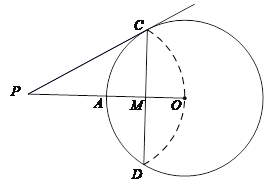
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球:C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如两个统计图.请结合图中的信息解答下列问题:
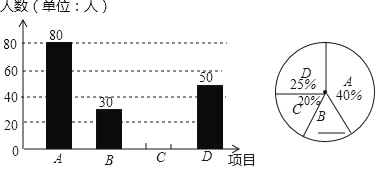
(1)本次共调查了多少名学生?
(2)请将两个统计图补充完整.
(3)求图中“A”层次所在扇形的圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com