
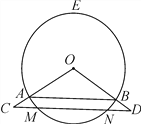
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3![]() -3,CD∥AB,并与弧AB相交于点M、N.
-3,CD∥AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若sin∠C=![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
【答案】(1)线段OD的长为![]() ;
;
(2)弦MN的长为3;
(3)优弧MEN的长度![]() .
.
【解析】分析:(1)由OA=OB得:OA=OB,根据CD∥AB可知,∠OAB=∠C, ∠D=∠OBA,推出∠C=∠D,最后求出OD的长;(2)过O作OF⊥CD,连接OM,由垂径定理可知MF=![]() MN,再根据sin∠C=
MN,再根据sin∠C=![]() 可求出OF的长,利用勾股定理即可求出ME的长,进而求出答案.(3)由OM=ON=MN得到△OMN是等边三角形,利用弧长公式求解.
可求出OF的长,利用勾股定理即可求出ME的长,进而求出答案.(3)由OM=ON=MN得到△OMN是等边三角形,利用弧长公式求解.
本题解析:(1)∵OA=OB ∴OA=OB
∵CD∥AB ∴∠OAB=∠C, ∠D=∠OBA
∴∠C=∠D ∴OD=OC=OA+AC=![]()
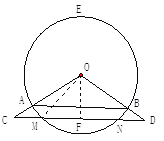 (2)过O作OF⊥MN于点F,连结OM。
(2)过O作OF⊥MN于点F,连结OM。
∵![]() ,OC=
,OC=![]() ∴OF=
∴OF=![]() ∵OM=3 根据勾股定理得MF=
∵OM=3 根据勾股定理得MF=![]()
由垂径定理得MN=3, (3)由(2)可得△OMN是等边三角形,∴∠MON=60°
∴优弧MEN的长度=![]()


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC. 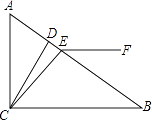
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
A.AD=BD
B.BD=CD
C.∠A=∠BED
D.∠ECD=∠EDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm.从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1cm/s,动点P沿A﹣B﹣﹣C﹣﹣E的方向运动,到点E停止;动点Q沿B﹣﹣C﹣﹣E﹣﹣D的方向运动,到点D停止,设运动时间为xs,△PAQ的面积为ycm2,(这里规定:线段是面积为0的三角形)

解答下列问题:
(1)当x=2s时,y= cm2;当x=![]() s时,y= cm2.
s时,y= cm2.
(2)当5≤x≤14 时,求y与x之间的函数关系式.
(3)当动点P在线段BC上运动时,求出![]() 时x的值.
时x的值.
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2=2﹣3x化成ax2+bx+c=0(a≠0)的形式后,a,b,c的值分别为( )
A. 0,2,﹣3B. 1,2,﹣3C. 1,﹣2,3D. 1,3,﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E,F.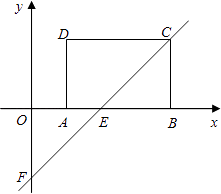
(1)求矩形ABCD的顶点A,B,C,D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x﹣2上一点,若S△POE=5,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com