
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E,F.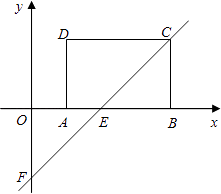
(1)求矩形ABCD的顶点A,B,C,D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x﹣2上一点,若S△POE=5,求点P的坐标.
【答案】
(1)
解:∵AD=BC=2,
故可设点C的坐标为(m,2),
又∵点C在直线y=x﹣2上,
∴2=m﹣2,
解得:m=4,即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
故可得点A,B,D的坐标分别为(1,0)、(4,0)、(1,2)
(2)
解:直线y=x﹣2与x轴、y轴坐标分别为E (2,0)、F (0,﹣2),
∴OF=OE=BC=BE=2,
在RT△OEF和RT△BEC中, 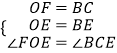
故可得△OEF≌△BEC
(3)
解:设点P的坐标为(xp,yp),则S△POE= ![]() ×OE×|yp|=
×OE×|yp|= ![]() ×2×|yp|=5,
×2×|yp|=5,
解得:yp=±5,
①当yp=5时,xp=7;②当yp=﹣5时,xp=﹣3,
故点P的坐标为(7,5)或(﹣3,﹣5)
【解析】(1)根据题意可得点C的纵坐标为2,代入函数解析式可得出点C的坐标,结合矩形的性质可得出A、B、D的坐标;(2)先求出OE、OF的长度,从而利用SAS证明△OEF≌△BEC即可.(3)设点P的坐标为(xp , yp),则可表示出S△POE= ![]() ×OE×|yp|,解出xp的值讨论即可.
×OE×|yp|,解出xp的值讨论即可.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
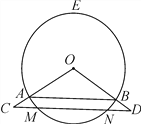
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3![]() -3,CD∥AB,并与弧AB相交于点M、N.
-3,CD∥AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若sin∠C=![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在式子-3<0,4x+3y>0,x=3,a2+2a+1≤8,x2+2xy+y2,x≠5,x2≥0中,不等式有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值
②求:24m﹣6n的值
(2)已知2×8x×16=223 , 求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中间的小正方形(即阴影部分)面积可表示为 .
(2)观察图2,请你写出三个代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系式: .
(3)根据(2)中的结论,若x+y=﹣6,xy=2.75,则x﹣y= .
(4)有许多代数恒等式可以用图形的面积来表示.如图3所示,它表示了(2m+n)(m+n)=2m2+3mn+n2 . 试画出一个几何图形,使它的面积能表示为(m+n)(m+2n)=m2+3mn+2n2 . 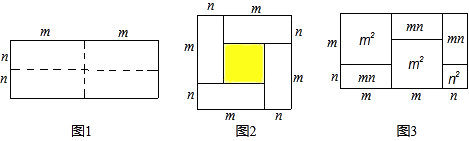
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店将某种服装按成本价每件a元提高50%标价,又以8折优惠卖出,则这种服装每件的售价是( )
A.0.8a元
B.0.4a元
C.1.2a元
D.1.5a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣4、- ![]() 、0、
、0、 ![]() 、4这五个数中,任取一个数作为a的值,恰好使得关于x的一元二次方程2ax2﹣6x﹣1=0有两个不相等的实数根,且使两个根都在﹣1和1之间(包括﹣1和1),则取到满足条件的a值的概率为 .
、4这五个数中,任取一个数作为a的值,恰好使得关于x的一元二次方程2ax2﹣6x﹣1=0有两个不相等的实数根,且使两个根都在﹣1和1之间(包括﹣1和1),则取到满足条件的a值的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com