
【题目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分线.
(1)求∠DCE的度数.
(2)若∠CEF=135°,求证:EF∥BC. 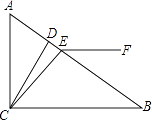
【答案】
(1)解:∵∠B=30°,CD⊥AB于D,
∴∠DCB=90°﹣∠B=60°.
∵CE平分∠ACB,∠ACB=90°,
∴∠ECB= ![]() ∠ACB=45°,
∠ACB=45°,
∴∠DCE=∠DCB﹣∠ECB=60°﹣45°=15°
(2)解:∵∠CEF=135°,∠ECB= ![]() ∠ACB=45°,
∠ACB=45°,
∴∠CEF+∠ECB=180°,
∴EF∥BC
【解析】(1)由图示知∠DCE=∠DCB﹣∠ECB,由∠B=30°,CD⊥AB于D,利用内角和定理,求出∠DCB的度数,又由角平分线定义得∠ECB= ![]() ∠ACB,则∠DCE的度数可求;(2)根据∠CEF+∠ECB=180°,由同旁内角互补,两直线平行可以证明EF∥BC.
∠ACB,则∠DCE的度数可求;(2)根据∠CEF+∠ECB=180°,由同旁内角互补,两直线平行可以证明EF∥BC.


科目:初中数学 来源: 题型:
【题目】在如图所示的4×4方格中,每个小方格的边长都为1
(1)在图(1)中画出长度为 ![]() 的线段,要求线段的端点在格点上;
的线段,要求线段的端点在格点上;
(2)在图(2)中画出一个三条边长分别为3,2 ![]() ,
, ![]() 的三角形,使它的端点都在格点上.
的三角形,使它的端点都在格点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题. 大家知道 ![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 ![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1< ![]() <2,所以
<2,所以 ![]() 的整数部分为1,将
的整数部分为1,将 ![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分 ![]() ﹣1,根据以上的内容,解答下面的问题:
﹣1,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是 , 小数部分是;
的整数部分是 , 小数部分是;
(2)1+ ![]() 的整数部分是 , 小数部分是;
的整数部分是 , 小数部分是;
(3)若设2+ ![]() 整数部分是x,小数部分是y,求x﹣
整数部分是x,小数部分是y,求x﹣ ![]() y的值.
y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.x=1是不等式-2x<1的解集
B.x=-3是不等式-x<1的解集
C.x>-2是不等式-2x<1的解集
D.不等式-x<1的解集是x<-1
查看答案和解析>>
科目:初中数学 来源: 题型:
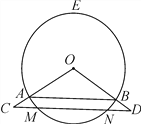
【题目】如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=3,AC=3![]() -3,CD∥AB,并与弧AB相交于点M、N.
-3,CD∥AB,并与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若sin∠C=![]() ,求弦MN的长;
,求弦MN的长;
(3)在(2)的条件下,求优弧MEN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a-3=0.
(1) 若该方程有一根是-2,求另一根;
(2) 求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com