
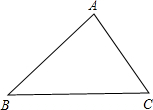
 将△ABC沿BC方向平移,使点B移到点C
将△ABC沿BC方向平移,使点B移到点C分析 (1)延长BC到C′,过点A作AA′∥BC且使AA′=BC,然后连接A′、C、C′即可;
(2)根据平移的性质可得AB∥A′C,再根据两直线平行,内错角相等解答;
(3)根据两直线平行,同位角相等可得∠B=∠A′CC′,再根据平角的定义证明.
解答 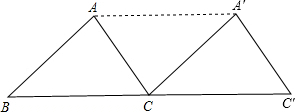 解:(1)△A′CC′如图所示;
解:(1)△A′CC′如图所示;
(2)∠ACA′=∠A,
理由如下:由平移的性质得,AB∥A′C,
所以,∠ACA′=∠A;
(3)∵AB∥A′C,
∴∠B=∠A′CC′,
∵∠ACA′+∠A′CC′+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
点评 本题考查了利用平移变换作图,平行线的性质,熟练掌握平移的性质准确确定出对应点的位置是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 多边形的内角和与外角和
多边形的内角和与外角和查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小丽参加本次语文考试,成绩是150分 | |
| B. | 某篮球运动员远距离投篮一次,投中3分 | |
| C. | 打开电视机,CCTV第五套节目正在播放羽毛球比赛 | |
| D. | 口袋中装有2个白球和1个黑球,从中摸出2个球,其中必有白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
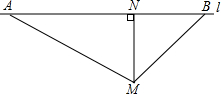 如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.
如图,根据道路管理规定,在某笔直的大道AB上行驶的车辆,限速60千米/时,已知测速站点M距大道AB的距离MN为30米,现有一辆汽车从A向B方向匀速行驶,测得此车从A点行驶到B点所用时间危机6秒,∠AMN=60°,∠BMN=45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com