
如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.

(1)证明见解析
(2)△FED的面积为2.
【解析】
试题分析:(1)根据平行四边形的性质,可知AB//CD,可是∠ABE=∠F,又AE=DE,∠BEA=∠FED由AAS可证明△ABE≌△DFE,可得FD=AB
(2)由AD//BC可得∴△FED∽△FBC,由相似三角形的性质可知S△FED:S△FBC=(FE:FB)2,根据(1)可得BE=EF,S△FDE=S平行四边形ABCD,从而可得△FED的面积为2.
试题解析:(1)∵在平行四边形ABCD中,E是AD边上的中点,∴AE=ED,∠ABE=∠F,
在△ABE和△DFE中 ,∴△ABE≌△DFE(AAS),∴FD=AB;
,∴△ABE≌△DFE(AAS),∴FD=AB;
(2)∵DE∥BC,∴△FED∽△FBC,∵△ABE≌△DFE,
∴BE=EF,S△FDE=S平行四边形ABCD,∴ ,∴
,∴ ,∴
,∴ ,
,
∴△FED的面积为:2.
考点:1、平行四边形的性质;2、全等三角形的判定;3、相似三角形的判定和性质


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:解答题
某经销商从市场得知如下信息:
| A品牌手表 | B品牌手表 |
进价(元/块) | 700 | 100 |
售价(元/块) | 900 | 160 |
他计划用4万元资金一次性购进这两种品牌手表共100块,设该经销商购进A品牌手表x块,这两种品牌手表全部销售完后获得利润为y元.
(1)试写出y与x之间的函数关系式;
(2)若要求全部销售完后获得的利润不少于 1.26万元,该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
如图,已知抛物线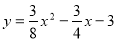 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:选择题
汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数关系的大致图象是( )

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:解答题
在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;(2)设计的整个图案是某种对称图形.王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
名称 | 四等分圆的面积 | ||
方案 | 方案一 | 方案二 | 方案三 |
选用的工具 | 带刻度的三角板 | 量角器 | 带刻度的三角板、圆规 |
画出示意图 |
|
|
|
简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. |
|
|
指出对称性 | 既是轴对称图形又是中心对称图形 |
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com