
如图,已知抛物线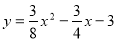 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.

(1)A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);
(2)M点坐标为(2,﹣3)或(1+ ,3)或(1﹣
,3)或(1﹣ ,3);
,3);
(3)结论:在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).
【解析】
试题分析:(1)令Y=0,X=0就可以得到
根据已知先求得对称轴,由于△MAD的面积与△CAD的面积相等,所以有两种情况,一种是点M在X轴下方,此时点M与点C关于对称轴对称,另一种是点M在X轴上方,由于面积相等,而AD是两个三角形公用的,所以可知点M的纵坐标为3,将Y=3代入解析式就可求得.
分情况讨论,一种是BC、AP为底,此时P点与D点重合;一种是AB、CP为底,此时要先求出AB所在直线的解析式,然后根据互相平行的两直线的K值相等,求出CP的解析式,与二次函数的解析式联立,得到方程组,求解即可得到。
试题解析:(1)∵y= x2﹣
x2﹣ x﹣3,∴当y=0时,
x﹣3,∴当y=0时, x2﹣
x2﹣ x﹣3=0,
x﹣3=0,
解得x1=﹣2,x2=4.当x=0,y=﹣3.
∴A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);
(2)∵y= x2﹣
x2﹣ x﹣3,∴对称轴为直线x=
x﹣3,∴对称轴为直线x= =1.
=1.
∵AD在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,﹣3),∴M点坐标为(2,﹣3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.当y=3时, x2﹣
x2﹣ x﹣3=3,解得x1=1+
x﹣3=3,解得x1=1+ ,x2=1﹣
,x2=1﹣ ,
,
∴M点坐标为(1+ ,3)或(1﹣
,3)或(1﹣ ,3).
,3).
综上所述,所求M点坐标为(2,﹣3)或(1+ ,3)或(1﹣
,3)或(1﹣ ,3);
,3);
(3)结论:存在.

如图所示,在抛物线上有两个点P满足题意:
①若BC∥AP1,此时梯形为ABCP1.
由点C关于抛物线对称轴的对称点为B,可知BC∥x轴,则P1与D点重合,
∴P1(﹣2,0).∵P1A=6,BC=2,∴P1A≠BC,∴四边形ABCP1为梯形;
②若AB∥CP2,此时梯形为ABCP2.
∵A点坐标为(4,0),B点坐标为(2,﹣3),∴直线AB的解析式为y= x﹣6,
x﹣6,
∴可设直线CP2的解析式为y= x+n,将C点坐标(0,﹣3)代入,得b=﹣3,
x+n,将C点坐标(0,﹣3)代入,得b=﹣3,
∴直线CP2的解析式为y= x﹣3.∵点P2在抛物线y=
x﹣3.∵点P2在抛物线y= x2﹣
x2﹣ x﹣3上,
x﹣3上,
∴ x2﹣
x2﹣ x﹣3=
x﹣3= x﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,
x﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,
∴点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,∴P2(6,6).
∵AB∥CP2,AB≠CP2,∴四边形ABCP2为梯形.
综上所述,在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).
考点:1、二次函数的性质;2、等积三角形;3、梯形;4、解方程


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:填空题
如图,A(4,0),B(3,3),以AO,AB为边作平行四边形OABC,则经过C点的反比例函数的解析式为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:选择题
南宁东高铁火车站位于南宁市青秀区凤岭北路,火车站总建筑面积约为267000平方米,其中数据267000用科学记数法表示为 ( )
(A)26.7×10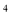 (B)2.67×10
(B)2.67×10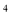 (C)2.67×10
(C)2.67×10 (D)0.267×10
(D)0.267×10
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:选择题
函数y=ax2+1与 (a≠0)在同一平面直角坐标系中的图象可能是( )
(a≠0)在同一平面直角坐标系中的图象可能是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:选择题
在平面直角坐标系中,点M(﹣2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
已知关于x的方程 .
.
(1)当该方程的一个根为1时,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )

A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,内错角相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com