
在数学活动课上,王老师发给每位同学一张半径为6个单位长度的圆形纸板,要求同学们:(1)从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具,把圆形纸板分成面积相等的四部分;(2)设计的整个图案是某种对称图形.王老师给出了方案一,请你用所学的知识再设计两种方案,并完成下面的设计报告.
名称 | 四等分圆的面积 | ||
方案 | 方案一 | 方案二 | 方案三 |
选用的工具 | 带刻度的三角板 | 量角器 | 带刻度的三角板、圆规 |
画出示意图 |
|
|
|
简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. |
|
|
指出对称性 | 既是轴对称图形又是中心对称图形 |
|
|
见解析
【解析】
试题分析:方案二:根据圆是轴对称图形,(1)以点O为圆心,以3个单位长度为半径作圆;(2)在大⊙O上依次取三等分点A、B、C;(3)连接OA、OB、OC.则小圆O与三等份圆环把⊙O的面积四等分.
方案三:根据既是轴对称图形又是中心对称图形,(1)作⊙O的一条直径AB;(2)分别以OA、OB的中点为圆心,以3个单位长度为半径作⊙O1、⊙O2;则⊙O1、⊙O2和⊙O中剩余的两部分把⊙O的面积四等分。
试题解析:
名称 | 四等分圆的面积 | ||
方案 | 方案一 | 方案二 | 方案三 |
选用的工具 | 带刻度的三角板 | 带刻度三角板、量角器、圆规. | 带刻度三角板、圆规. |
画出示意图 |
|
|
|
简述设计方案 | 作⊙O两条互相垂直的直径AB、CD,将⊙O的面积分成相等的四份. | (1)以点O为圆心,以3个单位长度为半径作圆; (2)在大⊙O上依次取三等分点A、B、C; (3)连接OA、OB、OC. 则小圆O与三等份圆环把⊙O的面积四等分. | 作⊙O的一条直径AB; 分别以OA、OB的中点为圆心,以3个单位长度为半径作⊙O1、⊙O2; 则⊙O1、⊙O2和⊙O中剩余的两部分把⊙O的面积四等分。 |
指出对称性 | 既是轴对称图形又是中心对称图形. | 轴对称图形 | 既是轴对称图形又是中心对称图形. |
考点:轴对称图形;中心对称图形;圆的性质.


科目:初中数学 来源:2014年初中毕业升学考试(广东汕尾卷)数学(解析版) 题型:解答题
如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:选择题
下列事件中是必然事件是( )
A、明天太阳从西边升起
B、篮球队员在罚球线投篮一次,未投中
C、实心铁球投入水中会沉入水底
D、抛出一枚硬币,落地后正面向上
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )

A.垂直 B.相等 C.平分 D.平分且垂直
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是( )

A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,内错角相等
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:填空题
如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD 经过点C,如图(2)所示,则图(2)中四边形OGCF与△OCH面积的比为 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(山东济宁卷)数学(解析版) 题型:选择题
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程 的两根,且a < b, 则a、b、m、n 的大小关系是( )
的两根,且a < b, 则a、b、m、n 的大小关系是( )
A.m < a < b< n B.a < m < n < b C.a < m < b< n D.m < a < n < b
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(安徽卷)数学(解析版) 题型:填空题
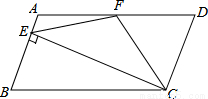
如图,在平行四边ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 (把所有正确结论的序号都填在横线上)
(1)∠DCF=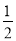 ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川达州卷)数学(解析版) 题型:解答题
达州市凤凰小学位于北纬21°,此地一年中冬至日正午时刻,太阳光与地面的夹角最小,约为35.5°;夏至日正午时刻,太阳光的夹角最大,约为82.5°.己知该校一教学楼窗户朝南,窗高207cm,如图(1).请你为该窗户设计一个直角形遮阳棚BCD,如图(2),要求最大限度地节省材料,夏至日正午刚好遮住全部阳光,冬至日正午能射入室内的阳光没有遮挡.

(1)在图(3)中画出设计草图;
(2)求BC、CD的长度(结果精确到个位)(参考数据:sin35.5°≈0.58,cos35.5°≈0.81,tan35.5°≈0.71,sin82.5°≈0.99,cos82.5°≈0.13,tan82.5°≈7.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com