
【题目】下列各组数中,数值相等的是( )
A.﹣23和(﹣2)3
B.32和23
C.﹣32和(﹣3)2
D.﹣(3×2)2和﹣3×22
科目:初中数学 来源: 题型:
【题目】某开发公司要生产若干件新产品,需要精加工后,才能投放市场,现有红星和巨星两个加工厂都想加工这批产品,已知红星厂单独加工比巨星厂单独加工这批产品多用![]() 天,红星厂每天可加工
天,红星厂每天可加工![]() 件产品,巨星厂每天可加工
件产品,巨星厂每天可加工![]() 件产品,公司需付红星厂每天加工费
件产品,公司需付红星厂每天加工费![]() 元,巨星厂每天加工费
元,巨星厂每天加工费![]() 元.
元.
(![]() )这个公司要加工多少件新产品?
)这个公司要加工多少件新产品?
(![]() )在加工过程中,公司需令派一名工程师每天到厂家进行指导,并负担每天
)在加工过程中,公司需令派一名工程师每天到厂家进行指导,并负担每天![]() 元的午餐补助费,公司制定的方案中,选择一种既省钱又省时的加工方案.
元的午餐补助费,公司制定的方案中,选择一种既省钱又省时的加工方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
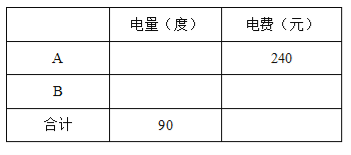
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
图1是边长分别为a和b(a>b)的两个等边三角形纸片ABC和C′DE叠放在一起(C与C′重合)的图形.
操作与证明:
(1)操作:固定△ABC,将△C′DE绕点C按顺时针方向旋转30°,连接AD,BE,如图2;在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
(2)操作:若将图1中的△C′DE,绕点C按顺时针方向任意旋转一个角度α,连接AD,BE,如图3;在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论;
猜想与发现:
(3)根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大是多少?当α为多少度时,线段AD的长度最小是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到 “分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
【提出问题】三个有理数![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
【解决问题】
解:由题意,得![]() 三个有理数都为正数或其中一个为正数,另两个为负数.
三个有理数都为正数或其中一个为正数,另两个为负数.
①![]() 都是正数,即
都是正数,即![]() 时,则
时,则![]() ;
;
②当![]() 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设![]() ,则
,则![]() .
.
综上所述, ![]() 值为3或-1.
值为3或-1.
【探究】请根据上面的解题思路解答下面的问题:
(1)三个有理数![]() 满足
满足![]() ,求
,求![]() 的值;
的值;
(2)若![]() 为三个不为0的有理数,且
为三个不为0的有理数,且![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜花饼是云南的特色小吃,也是中国四大月饼流派滇式月饼的经典代表之一,深受人们喜爱.现某车间要为鲜花饼制作长方体包装盒,已知一个盒子由一个盒身和两个盒底构成,每一张纸板可以做盒身10个或盒底30个.现有纸板100张,应用多少张制作盒身,多少张制作盒底,才能使盒身和盒底正好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气魄雄伟的大礼堂座落在渝中区学田湾,它是一座仿古民族建筑.“五一”期间,小明和妈妈到重庆大礼堂参观游玩.参观结束后,穿过人民广场到达A处,回望礼堂,更显气势雄伟,金碧辉煌.此时,在A点观察到礼堂顶端的仰角为30°,沿着坡度为1:3的斜坡AB走一段距离到达B点,观察到礼堂顶端 的仰角是22°,测得点A与BC之间的水平距离![]() 米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:
米,则大礼堂的高度DE为( )米.(精确到1米.参考数据: ![]() ,
, ![]() .)
.)
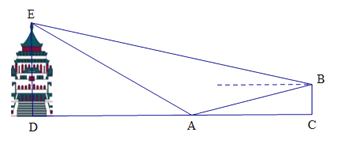
A. 58 B. 60 C. 62 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
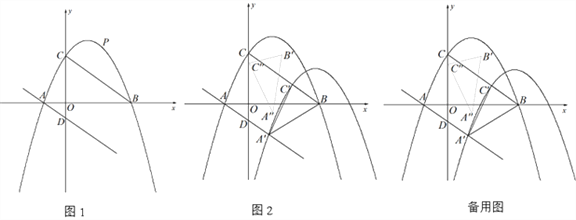
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD//BC交y轴于点D.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD//BC交y轴于点D.
(1)求平行线AD、BC之间的距离;
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
(3)如图2,将抛物线以每秒![]() 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作![]() ,当
,当![]() 是以
是以![]() 为底边的等腰三角形时,将等腰
为底边的等腰三角形时,将等腰![]() 绕点D逆时针旋转一周,记旋转中的
绕点D逆时针旋转一周,记旋转中的![]() 为
为![]() ,若直线
,若直线![]() 与y轴交于点K,直线
与y轴交于点K,直线![]() 与直线AD交于点I,当
与直线AD交于点I,当![]() 是以KI为底边的等腰三角形时,求出
是以KI为底边的等腰三角形时,求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com