
【题目】春季流感爆发,有一人患了流感,经过两轮传染后共有![]() 人患了流感,
人患了流感,
(1)每轮传染中平均一个人传染了几个人?
(2)经过三轮传染后共有多少人患了流感?
【答案】(1)每轮传染中平均一个人传染8个人;(2)经过三轮传染后共有729人会患流感.
【解析】
(1)设每轮传染中平均一个人传染x个人,根据经过两轮传染后共有81人患了流感,即可得出关于x的一元二次方程,解之取其正值即可得出结论;
(2)根据经过三轮传染后患流感的人数=经过两轮传染后患流感的人数+经过两轮传染后患流感的人数×8,即可求出结论.
解:(1)设每轮传染中平均一个人传染x个人,
根据题意得:1+x+x(x+1)=81,
整理,得:x2+2x-80=0,
解得:x1=8,x2=-10(不合题意,舍去).
答:每轮传染中平均一个人传染8个人.
(2)81+81×8=729(人).
答:经过三轮传染后共有729人会患流感.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
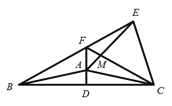
【题目】已知:如图,在等腰三角形ABC中,120BAC180,ABAC,ADBC于点D,以AC为边作等边三角形ACE,ACE与ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.
(1)求EFC的度数;
(2)求证:FE+FA=FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:

①AD和EF互相垂直平分;
②AE=AF;
③当∠BAC=90°时,AD=EF;
④DE是AB的垂直平分线.
其中正确的是_________________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
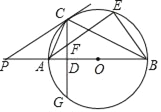
【题目】如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D
(1)求证:PC是⊙O的切线;
(2)求证:![]() ;
;
(3)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P=![]() ,CF=5,求BE的长.
,CF=5,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+4)x+(3﹣n).
(1)当m、n是什么数时,y随x的增大而增大;
(2)当m、n是什么数时,函数图象经过原点;
(3)若图象经过一、二、三象限,求m、n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“我运动,我快乐”的技能比赛培训活动中,在相同条件下,对甲、乙两名同学的“单手运球”项目进行了5次测试,测试成绩(单位:分)如下:根据右图判断正确的是( )

A.甲成绩的平均分低于乙成绩的平均分;
B.甲成绩的中位数高于乙成绩的中位数;
C.甲成绩的众数高于乙成绩的众数;
D.甲成绩的方差低于乙成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届全国青年运动会将于2019年8月在太原开幕,这是山西历史上第一次举办全国大型综合性运动会,必将推动我市全民健康理念的提高.某体育用品商店近期购进甲、乙两种运动衫各50件,甲种用了2000元,乙种用了2400元.商店将甲种运动衫的销售单价定为60元,乙种运动衫的销售单价定为88元.该店销售一段时间后发现,甲种运动衫的销售不理想,于是将余下的运动衫按照七折销售;而乙种运动衫的销售价格不变.商店售完这两种运动衫至少可获利2460元,求甲种运动衫按原价销售件数的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com