
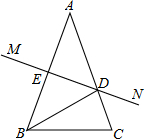
 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.若∠DBC=33°,∠A的度数为38°.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”| A. | 3(x+4)=4(x+1) | B. | 3x+4=4x+1 | C. | 3(x-4)=4(x-1) | D. | $\frac{x}{3}-4=\frac{x}{4}-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
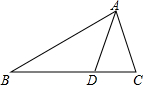 如图,在△ABC中,∠B=30°,∠C=70°,AD是△ABC的一条角平分线,则∠CAD的度数为( )
如图,在△ABC中,∠B=30°,∠C=70°,AD是△ABC的一条角平分线,则∠CAD的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
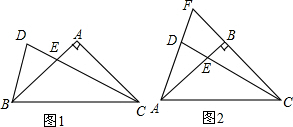
 如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1,则∠P1=110°,D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2,…按这样规律,则∠P2016=110°.
如图,若∠B=40°,A、C分别为角两边上的任意一点,连接AC,∠BAC与∠ACB的平分线交于点P1,则∠P1=110°,D、F也为角两边上的任意一点,连接DF,∠BFD与∠FDB的平分线交于点P2,…按这样规律,则∠P2016=110°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com