
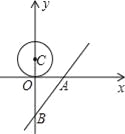
����Ŀ����ƽ��ֱ������ϵ�У���C������Ϊ��0��1.5�������ǰ��Ե�CΪԲ�ģ��뾶Ϊ1.5��Բ��Ϊ��C������Ȧ��Բ���ϵ�ÿһ���������C��һ�����ѣ�
��1��д����C�������������ꣻ
��2��ֱ��l�Ľ���ʽ��y=![]() x��4����x�ᡢy��ֱ���A��B���㣬Բ��C�ӵ㣨0��1.5����ʼ��ÿ��0.5����λ���ٶ�����y�������˶�������C������Ȧ�к�������ֱ����ʱ��ֱ�߽�����Ӱ�죬���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ�䣻
x��4����x�ᡢy��ֱ���A��B���㣬Բ��C�ӵ㣨0��1.5����ʼ��ÿ��0.5����λ���ٶ�����y�������˶�������C������Ȧ�к�������ֱ����ʱ��ֱ�߽�����Ӱ�죬���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ�䣻
��3��������y=ax2+bx+c��ԭ��O�͵�A���Ҷ���Dǡ��Ϊ��C�ĺ��ѣ�����OD��EΪ��C��һ�㣬����DOE������ʱ�����E�����꣬��ʱ��DOE������Ƕ��٣�
���𰸡���1���㣨0��0������0��3��Ϊ��C�ĺ��ѣ���2���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ��Ϊ6��t��16����3������DOE������ʱ����E������Ϊ����![]() ��
�� ![]() ������ʱ��DOE�������
������ʱ��DOE�������![]() ��
��
�������������������1��������Ȧ�Լ����ѵĶ��壬���ͼ�Σ����ɵó����ۣ���2����Բ��C�����˶���t�룬���C������Ϊ��0��1.5��0.5t�������ݺ��ѵĶ��壬��ϵ�C��ֱ��l�ľ���С�ڵ���1.5�����ɵó�����ʱ��t�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�̼��ɵó����ۣ���3�����ݶ��κ����������ҳ������ߵĶԳ��ᣬ��Ϻ���ͼ���Լ����ѵĶ����ҳ���D�����ꣻ����OD������C��CM��OD�ڵ�M���ӳ�MC��ԲC�ڵ�E������EO��ED��ͨ��������������ֱ������������߶�EM�ij����ٽ�������ε������ʽ�������S��DOE��ֵ���ɵ�C��M����������ô���ϵ�������ֱ��CM�Ľ���ʽ�������E�����꣬�ٽ�������ľ��빫ʽ���������E�����꣬����ý⣮
�����������1��1.5��1.5=0��1.5+1.5=3��
���㣨0��0������0��3������C�ľ���Ϊ1.5��
���㣨0��0������0��3��Ϊ��C�ĺ��ѣ�
��2����Բ��C�����˶���t�룬���C������Ϊ��0��1.5��0.5t����
ֱ��l��y=![]() x��4�ɱ���Ϊ4x��3y��12=0��
x��4�ɱ���Ϊ4x��3y��12=0��
��C��ֱ��l�ľ���d=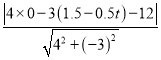 =|0.3t��3.3|��
=|0.3t��3.3|��
��ֱ����ԲCӰ��ʱ����d��1.5����|0.3t��3.3|��1.5��
��ã�6��t��16��
���ڵ�C�����˶��Ĺ����У�ֱ������Ӱ���ʱ��Ϊ6��t��16��
��3����y=![]() x��4��y=0����
x��4��y=0����![]() x��4=0��
x��4=0��
��ã�x=3������A������Ϊ��3��0����
�������⻭��ͼ�Σ���ͼ1��ʾ��
��������y=ax2+bx+c��ԭ��O�͵�A����O��0��0������A��3��0����
�������ߵĶԳ���Ϊx=![]() =1.5��
=1.5��
����Dǡ��Ϊ��C�ĺ��ѣ�
����D��������1.5��1.5����
����OD������C��CM��OD�ڵ�M���ӳ�MC��ԲC�ڵ�E������EO��ED����ʱS��DOE�����ͼ2��ʾ��
��OD��ԲC���ң�CM��OD��
����MΪ�߶�OD���е㣬
����M��������![]() ��
�� ![]() ����OM=
����OM=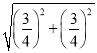 =
=![]() ��
��
��Rt��CMO��OM=![]() ��CO=1.5=
��CO=1.5=![]() ��
��
��CM=![]() =
=![]() ��
��
��CE=1.5=![]() ��EM=EC+CM��
��EM=EC+CM��
��EM=![]() ��
��
��ʱS��DOE=![]() ODEM=OMEM=
ODEM=OMEM=![]() ��
��![]() =
=![]() ��
��
��ֱ��CM�Ľ���ʽΪy=mx+n��
����C��������0��1.5������M��������![]() ��
�� ![]() ������0.75��0.75����
������0.75��0.75����
��![]() ����ã�
����ã� ![]() ��
��
��ֱ��CM�Ľ���ʽΪy=��x+1.5��
���E��������x����x+1.5����x��0����
��EC=![]() =1.5��
=1.5��
��x=��![]() ����x=
����x=![]() ����ȥ����
����ȥ����
����E����������![]() ��
�� ![]() ����
����
�ʵ���DOE������ʱ����E������Ϊ����![]() ��
�� ![]() ������ʱ��DOE�������
������ʱ��DOE�������![]() ��
��



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ���ڣ�ֱ��a��b�ཻ��O��b��c����a��c��λ�ù�ϵ�ǣ�������
A.ƽ��
B.�ཻ
C.�غ�
D.ƽ�л��غ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
��ֱ��l��һ��P��ֱ��l�Ĵ��߶εij��ȣ�������P��ֱ��l�ľ��룬����d��P��l����
������ƽ����![]() ��
��![]() ��ֱ��
��ֱ��![]() ������һ�㵽ֱ��
������һ�㵽ֱ��![]() �ľ��룬����������ƽ����
�ľ��룬����������ƽ����![]() ��
��![]() ֮��ľ��룬����d��
֮��ľ��룬����d��![]() ��
��![]() ����
����
����ֱ��![]() ��
��![]() �ཻ������d��
�ཻ������d��![]() ��
��![]() ��=0��
��=0��
����ֱ��![]() ��
��![]() �غϣ����Ƕ���d��
�غϣ����Ƕ���d��![]() ��
��![]() ��=0��
��=0��
��������![]() ��
��![]() ������ֱ��
������ֱ��![]() ��
��![]() ����������
����������![]() ��
��![]() �ġ�
�ġ�![]() ��
��![]() ��ؾ��롱���£�
��ؾ��롱���£�
d��![]() ��
��![]() |
|![]() ��
��![]() ��=d��
��=d��![]() ��
��![]() ��+d��
��+d��![]() ��
��![]() ��+d��
��+d��![]() ��
��![]() ��
��
��![]() ��4��0����
��4��0����![]() ��0��3����
��0��3����![]() ��y=x��
��y=x��![]() ��y=
��y=![]() ��
��![]() ��y=kx������������⣺
��y=kx������������⣺
��1��d��![]() ��
��![]() |
|![]() ��
��![]() ��= ��
��= ��
��2������k��0����d��![]() ��
��![]() |
|![]() ��
��![]() �����ʱ��k= ��
�����ʱ��k= ��
����k��0����ȷ��k��ֵ��ʹ��d��![]() ��
��![]() |
|![]() ��
��![]() �������˵�����ɣ�
�������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ھ���ABCD�У����ӶԽ���AC������ABC�Ƶ�B˳ʱ����ת90��õ���EFG����������ֱ��AB����ƽ�ƣ�ֱ��EG��BC���ڵ�H������AH��CG��
��1����ͼ������AB=BC����Fƽ�Ƶ��߶�BA��ʱ���߶�AH��CG��������������ϵ��λ�ù�ϵ��ֱ��д����IJ��룻
��2����ͼ������AB=BC����Fƽ�Ƶ��߶�BA���ӳ�����ʱ����1���еĽ����Ƿ��������˵�����ɣ�
��3����ͼ������AB=nBC��n��1��ʱ���Ծ���ABCD��������֪ͬ���ı任�������߶�AH��CG��������������ϵ��λ�ù�ϵ��ֱ��д����IJ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
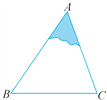
����Ŀ����ͼ��һ��������ģ�ߵ���Ӱ����������
(1)ֻҪ�Ӳ�����ģ��Ƭ�ж�������Щ�ߡ��ǣ��Ϳ��Բ���������ģ��Ƭ�����̼ӹ�һ����ԭ����ģ��ABC����״�ʹ�С��ȫ��ͬ��ģ��A��B��C�䣿���Ҫ˵�����ɣ�
(2)����ģ�ߡ�A��B��C���ͼ��(Ҫ�߹���ͼ��������ͼ�ۼ�����д������֤��)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ϣ��һ���ڱ�ת����2180000�Σ�������2180000�ÿ�ѧ��������ʾΪ�� ��
A. 2.18��105 B. 2.18��106 C. 21.8��106 D. 21.8��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� С����һ��ѧУ����ӵĶ�Ա������������������ͳ�ƣ�С��ÿ������������Ϊ15%�������콫�μ�һ��ѧУ����ӱ���������˵����ȷ���ǣ�������
A.С������϶�����B.С������ÿ����15�αؽ���1��
C.С�������п��ܽ���D.С������һ�����ܽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�Σ�����Գ�ͼ�ε��������ĶԳ�ͼ�ε��ǣ� ��
A.������
B.ƽ���ı���
C.����������
D.Բ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com