
【题目】阅读材料:
①直线l外一点P到直线l的垂线段的长度,叫做点P到直线l的距离,记作d(P,l);
②两条平行线![]() ,
,![]() ,直线
,直线![]() 上任意一点到直线
上任意一点到直线![]() 的距离,叫做这两条平行线
的距离,叫做这两条平行线![]() ,
,![]() 之间的距离,记作d(
之间的距离,记作d(![]() ,
,![]() );
);
③若直线![]() ,
,![]() 相交,则定义d(
相交,则定义d(![]() ,
,![]() )=0;
)=0;
④若直线![]() ,
,![]() 重合,我们定义d(
重合,我们定义d(![]() ,
,![]() )=0,
)=0,
对于两点![]() ,
,![]() 和两条直线
和两条直线![]() ,
,![]() ,定义两点
,定义两点![]() ,
,![]() 的“
的“![]() ,
,![]() 相关距离”如下:
相关距离”如下:
d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )
)
设![]() (4,0),
(4,0),![]() (0,3),
(0,3),![]() :y=x,
:y=x,![]() :y=
:y=![]() ,
,![]() :y=kx,解决以下问题:
:y=kx,解决以下问题:
(1)d(![]() ,
,![]() |
|![]() ,
,![]() )= ;
)= ;
(2)①若k>0,则当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k= ;
)最大时,k= ;
②若k<0,试确定k的值,使得d(![]() ,
,![]() |
|![]() ,
,![]() )最大,请说明理由.
)最大,请说明理由.

【答案】(1) ![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)首先分别求出d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )的值各是多少,再把它们求和,求出d(
)的值各是多少,再把它们求和,求出d(![]() ,
,![]() |
|![]() ,
,![]() )的值是多少;然后分别求出d(
)的值是多少;然后分别求出d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )、d(
)、d(![]() ,
,![]() )的值各是多少,再把它们求和,求出d(
)的值各是多少,再把它们求和,求出d(![]() ,
,![]() |
|![]() ,
,![]() )的值是多少即可.
)的值是多少即可.
(2)①首先作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,连接
于点B,连接![]()
![]() 交
交![]() 于点C,然后根据
于点C,然后根据![]() A+
A+![]() B≤
B≤![]()
![]() ,可得当
,可得当![]()
![]() ⊥
⊥![]() 时,
时,![]() A+
A+![]() B的值最大,据此求出k的值是多少即可.
B的值最大,据此求出k的值是多少即可.
②首先作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,
于点B,![]() 、
、![]() 关于原点对称,
关于原点对称,![]() C⊥
C⊥![]() 于点C,
于点C,![]()
![]() 交
交![]() 于点D,然后根据
于点D,然后根据![]() B+
B+![]() C≤
C≤![]()
![]() ,可得当
,可得当![]()
![]() ⊥
⊥![]() 时,
时,![]() B+
B+![]() C取到最大值,据此求出k的值是多少即可.
C取到最大值,据此求出k的值是多少即可.
试题解析:(1)∵![]() (4,0),
(4,0),![]() (0,3),
(0,3),![]() :y=x,
:y=x,![]() :y=
:y=![]() ,
,
∴d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=![]() =
=![]() ;
;
∴d(![]() ,
,![]() |
|![]() ,
,![]() )= d(
)= d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=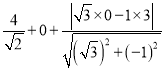 =
=![]() .
.
故答案为:![]() ;
;
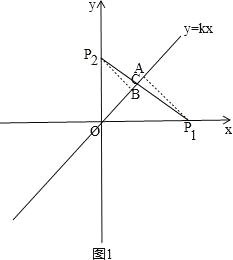
(2)①如图1,作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,连接
于点B,连接![]()
![]() 交
交![]() 于点C,
于点C,
d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=![]() A+
A+![]() B,
B,
∵![]() A≤
A≤![]() C,
C,![]() B≤
B≤![]() C,
C,
∴![]() A+
A+![]() B≤
B≤![]()
![]() ,
,
∴当![]()
![]() ⊥
⊥![]() 时,
时,
![]() A+
A+![]() B的最大值是:
B的最大值是:![]() =5,
=5,
此时k=tan∠O![]()
![]() =
=![]() =
=![]() ,
,
∴若k>0,当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k=
)最大时,k=![]() .
.
故答案为:![]() ;
;
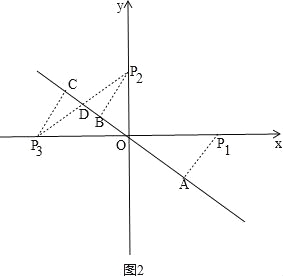
②如图2,作![]() A⊥
A⊥![]() 于点A,
于点A,![]() B⊥
B⊥![]() 于点B,
于点B,![]() 、
、![]() 关于原点对称,
关于原点对称,![]() C⊥
C⊥![]() 于点C,
于点C,![]()
![]() 交
交![]() 于点D,
于点D,
∵![]() 、
、![]() 关于原点对称,
关于原点对称,
∴![]() A=
A=![]() C,
C,
∴d(![]() ,
,![]() |
|![]() ,
,![]() )=d(
)=d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )+d(
)+d(![]() ,
,![]() )=
)=![]() A+
A+![]() B=
B=![]() B+
B+![]() C,
C,
∵![]() B≤
B≤![]() D,
D,![]() C≤
C≤![]() D,
D,
∴![]() B+
B+![]() C≤
C≤![]()
![]() ,
,
∴当![]()
![]() ⊥
⊥![]() 时,
时,
![]() B+
B+![]() C的最大值是:
C的最大值是:![]() =
=![]() =5,
=5,
此时k=﹣tan∠O![]()
![]() =
=![]() =
=![]() ,
,
∴若k<0,当d(![]() ,
,![]() |
|![]() ,
,![]() )最大时,k=
)最大时,k=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 同旁内角相等,两直线平行
B. 对角线互相平分的四边形是平行四边形
C. 相等的两个角是对顶角
D. 圆内接四边形对角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家今年刚成立的小型快递公司业务量逐月攀升,今年7月份和9月份完成投送的快递件数分别是20万件和24.2万件.若假设该公司每月投送的快递件数的增长率相同,则这家公司投送快递件数的月平均增长率为 ________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法: ① ![]() 没有立方根;
没有立方根;
②实数与数轴上的点一一对应;
③近似数3.20万,该数精确到千位;
④ ![]() 是分数;
是分数;
⑤近似数5.60所表示的准确数x的范围是:5.55≤x<5.65
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
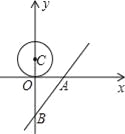
【题目】在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
(1)写出点C的两个好友坐标;
(2)直线l的解析式是y=![]() x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;
x﹣4,与x轴、y轴分别交于A、B两点,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当点C的朋友圈有好友落在直线上时,直线将受其影响,求在点C向下运动的过程中,直线受其影响的时间;
(3)抛物线y=ax2+bx+c过原点O和点A,且顶点D恰好为点C的好友,连接OD.E为⊙C上一点,当△DOE面积最大时,求点E的坐标,此时△DOE的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)2n﹣(2﹣n)+(6n﹣2),其中n=﹣2;
(2)﹣(3a2﹣4ab)+[a2﹣2(2a+2ab)],其中a=﹣2,b= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com