
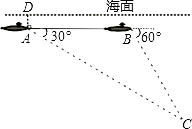
 一架空客A320-200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号)
一架空客A320-200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号) 分析 过点C作CE⊥DE,交AB于G,交DE于E根据∠GBC和∠BAC的度数,求出BC=AB的值,再根据特殊角的三角函数值求出GC,从而得出答案.
解答 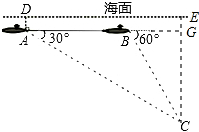 解:过点C作CE⊥DE,交AB于G,交DE于E,
解:过点C作CE⊥DE,交AB于G,交DE于E,
∵∠GBC=60°,∠BAC=30°,
∴∠BCA=∠BAC,
∴BC=AB=3000米,
∴CG=1500$\sqrt{3}$米,
∵GE=500米,
∴CE=1500$\sqrt{3}$+500(米),
答:海底疑似黑匣子C点处距离海面的深度为1500$\sqrt{3}$+500米.
点评 本题考查了解直角三角的应用,用到的知识点是仰角的定义和特殊角的三角函数值,要求学生能借助仰角构造直角三角形并解直角三角形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com