
分析 方程有实数根,则△≥0,建立关于m的不等式,求出m的取值范围.
解答 解:当m+1=0时,(m+1)x2-(m-1)x+$\frac{1}{4}$m=0变为2x-$\frac{1}{4}$=0
此时方程有实数根;
当m+1≠0时,
由题意知,△=(m-1)2-4×$\frac{1}{4}$m(m+1)=-3m+1≥0
∴m≤$\frac{1}{3}$.
∴当m≤$\frac{1}{3}$时,关于x的方程(m+1)x2-(m-1)x+$\frac{1}{4}$m=0有实数根.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
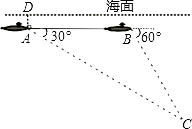 一架空客A320-200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号)
一架空客A320-200型客机2014年12月28日从印尼泗水飞往新加坡途中失事.我国政府马上派出舰船搜救,我海军一艘潜艇在海面下500米A点处测得仰角为30°正前方的海底有疑似黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有疑似黑匣子信号发出,求海底疑似黑匣子C点处距离海面的深度?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2+c2=a2 | B. | c2=3b2 | C. | 3a2=2c2 | D. | c2=2b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
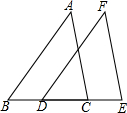 如图,在△ABC和△FDE中,若AB=FD,∠A=∠F,则只需增加条件AC=EF或者增加条件∠B=∠FDE,就可以证明△ABC≌△FDE.(每空只填一个即可)
如图,在△ABC和△FDE中,若AB=FD,∠A=∠F,则只需增加条件AC=EF或者增加条件∠B=∠FDE,就可以证明△ABC≌△FDE.(每空只填一个即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com