【题目】已知：如图，在平面直角坐标系
中，直线
分别与
、
轴交于点
，
，与反比例函数的图象分别交于点
、
，
轴于点
，
，
，
.
（1）求直线的解析式；
（2）求该反比例函数的解析式；
（3）连接
，
，求
的面积.
【答案】（1）
；（2）
；（3）8.
【解析】
（1）根据条件可得到A、B两点的坐标，然后利用待定系数法即可求出直线AB的解析式；
（2）利用平行线分线段成比例定理求出EO的长，得到C点的横坐标，代入直线AB的解析式确定C点坐标，然后利用待定系数法求反比例函数解析式；
（3）先解方程组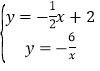
，得D点坐标，然后利用S△OCD=S△OAC+S△OAD进行计算．
（1）∵OB=4，OA=2，∴A点坐标为（0，2），B点坐标为（4，0）．
设直线AB的解析式为y=kx+b，把A（0，2）、B（4，0）代入，得：
，解得：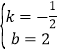
，∴直线AB的解析式为y
x+2；
（2）∵OA∥CE，∴EO：OB=CA：AB=1：2，∴EO
OB=2，∴C点的横坐标为﹣2．
把x=﹣2代入yx+2，得：y
（﹣2）+2=3，∴C点坐标为（﹣2，3）．
设反比例函数解析式为y
，把C（﹣2，3）代入，得：m=﹣2×3=﹣6，∴反比例函数解析式为y
；
（3）解方程组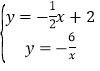，得
或
，则D（6，﹣1）．
S△OCD=S△OAC+S△OAD
2×2
2×6=8．
科目：初中数学 来源： 题型：
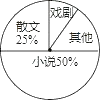
【题目】九年级一班开展了“读一本好书”的活动，班委会对学生阅读书籍的情况进行了问卷调查，问卷设置了“小说”“戏剧”“散文”“其他”四个类型，每位同学仅选一项，根据调查结果绘制了不完整的频数分布表和扇形统计图．
类别 | 频数（人数） | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息，解答下列问题：
（1）九年级一班有多少名学生？
（2）请补全频数分布表，并求出扇形统计图中“其他”类所占的百分比；
（3）在调查问卷中，甲、乙、丙、丁四位同学选择了“戏剧”类，现从以上四位同学中任意选出 2 名同学参加学校的戏剧兴趣小组，请用画树状图或列表法的方法，求选取的 2 人恰好是乙和丙的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
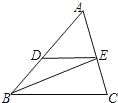
【题目】如图，在△ABC中，BE平分∠ABC交AC于点E，过点E作ED∥BC交AB于点D．
（1）求证：AEBC=BDAC；
（2）如果
=3，
=2，DE=6，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，半径为1的圆O1与半径为3的圆O2相内切，如果半径为2的圆与圆O1和圆O2都相切，那么这样的圆的个数是 （ ）
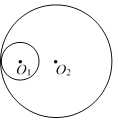
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC三个顶点的坐标分别为（1，2），（-2，3），（-1，0），把它们的横坐标和纵坐标都扩大到原来的2倍，得到点
， 
， 
．下列说法正确的是（ ）
A. △
与△ABC是位似图形，位似中心是点（1，0）
B. △
与△ABC是位似图形，位似中心是点（0，0）
C. △
与△ABC是相似图形，但不是位似图形
D. △
与△ABC不是相似图形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：为缓解交通拥堵问题，小李将上班方式由自驾车改为骑电动车．他从家到达上班地点，自驾车要走的路程为10千米，骑电动车要走的路程为8千米，已知小李自驾车的速度是骑电动车速度的1.5倍，他由自驾车改为骑电动车后，时间多用了6分钟.求小李自驾车和骑电动车的速度分别是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小琴的父母承包了一块荒山地种植一批梨树，今年收获一批金溪密梨，小琴的父母打算以m元/斤的零售价销售5000斤密梨；剩余的5000(m＋1)斤密犁以比零售价低1元的批发价批给外地客商，预计总共可赚得55 000元的毛利润．
（1）求小琴的父母今年共收获金溪密梨多少斤？
（2）若零售金溪密梨平均每天可售出200斤，每斤盈利2元．为了加快销售和获得较好的售价，采取了降价措施，发现销售单价每降低0.1元，平均每天可多售出40斤，应降价多少元？每天销售利润为600元．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，且抛物线经过A（-1，0），C（0，-5）两点，与x轴交于点B．
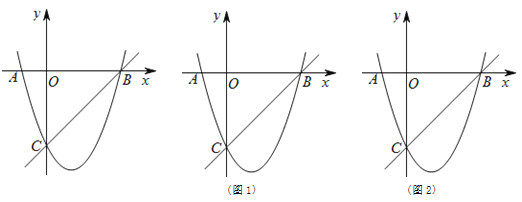
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）设点P为抛物线上的一个动点，连接PB、PC，若△BPC是以BC为直角边的直角三角形，求此时点P的坐标；
（3）在抛物线上BC段有另一个动点Q，以点Q为圆心作⊙Q，使得⊙Q与直线BC相切，在运动的过程中是否存在一个最大⊙Q. 若存在，请直接写出最大⊙Q的半径；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
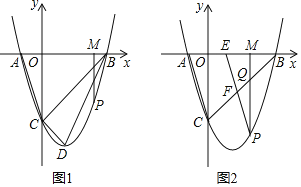
【题目】如图1，抛物线与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C（0，﹣3），抛物线顶点为D，连接AC，BC，CD，BD，点P是x轴下方抛物线上的一个动点，作PM⊥x轴于点M，设点M的横坐标为m．
（1）求抛物线的解析式及点D的坐标；
（2）试探究是否存在这样的点P，使得以P，M，B为顶点的三角形与△BCD相似？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）如图2，PM交线段BC于点Q，过点P作PE∥AC交x轴于点E，交线段BC于点F，请用含m的代数式表示线段QF的长，并求出当m为何值时QF有最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com