
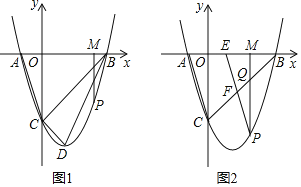
【题目】如图1,抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3),抛物线顶点为D,连接AC,BC,CD,BD,点P是x轴下方抛物线上的一个动点,作PM⊥x轴于点M,设点M的横坐标为m.
(1)求抛物线的解析式及点D的坐标;
(2)试探究是否存在这样的点P,使得以P,M,B为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由;
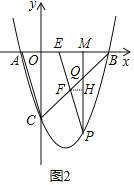
(3)如图2,PM交线段BC于点Q,过点P作PE∥AC交x轴于点E,交线段BC于点F,请用含m的代数式表示线段QF的长,并求出当m为何值时QF有最大值.
【答案】(1)y=x2﹣2x﹣3,(1,﹣4);(2)见解析;(3)见解析.
【解析】
(1)设抛物线解析式为:y=a(x+1)(x﹣3), 将C(0,-3),代入可求出解析式,根据抛物线的顶点坐标公式求出D点即可.
(2)由(1)可得BC=3![]() ,CD=
,CD=![]() ,BD=
,BD=![]() ,△BCD是直角三角形,∠BCD=90°,再分情况讨论:①当△PMB∽△BCD时,得点P(2,﹣3);②当△BMP∽△BCD时,点P的坐标为(﹣
,△BCD是直角三角形,∠BCD=90°,再分情况讨论:①当△PMB∽△BCD时,得点P(2,﹣3);②当△BMP∽△BCD时,点P的坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)设QF为y,作FH⊥PM于点H,先证明△FHP∽△AOC,得出PQ=![]() =2
=2![]() y,根据点B、C的坐标得到直线BC的表达式为:y=x﹣3,设点P(m,m2﹣2m﹣3),点Q(m,m﹣3),求出PQ=﹣m2+3m,即可解答.
y,根据点B、C的坐标得到直线BC的表达式为:y=x﹣3,设点P(m,m2﹣2m﹣3),点Q(m,m﹣3),求出PQ=﹣m2+3m,即可解答.
解:(1)设抛物线解析式为:y=a(x+1)(x﹣3),
将C(0,-3),代入可得:﹣3a=﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3,
根据顶点坐标公式得出D的坐标为![]()
∴点D的坐标为(1,﹣4);
(2)由(1)知,点B、C、D的坐标分别为(3,0)、(0,﹣3)、(1,﹣4),
则BC=3![]() ,CD=
,CD=![]() ,BD=
,BD=![]() ,
,
则△BCD是直角三角形,∠BCD=90°,
①当△PMB∽△BCD时,
则∠MPB=∠DBC,即:tan∠MPB=tan∠DBC=![]() ,
,
∵点M(m,0),则点P(m,m2﹣2m﹣3),
tan∠MPB=![]() ,
,
解得:m=2或3(舍去3),
故点P(2,﹣3);
②当△BMP∽△BCD时,
同理可得:点P(﹣![]() ,﹣
,﹣![]() );
);
故点P的坐标为:(2,﹣3)或(﹣![]() ,﹣
,﹣![]() );
);
(3)设QF为y,作FH⊥PM于点H,
∵OB=OC,∴∠OCB=∠OBC=45°
则FH=QH=![]() y,
y,
∵PE∥AC,PM∥OC,则∠PEM=∠HFP=∠CAO,
∴△FHP∽△AOC,
则PH=3FH=![]() y,
y,
∴PQ=![]() =2
=2![]() y,
y,
根据点B、C的坐标求出直线BC的表达式为:y=x﹣3,
则点P(m,m2﹣2m﹣3),点Q(m,m﹣3),
所以PQ=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,即:2![]() y=﹣m2+3m,
y=﹣m2+3m,
则y=![]() ,.
,.
∴当m=![]() 时,QF有最大值.
时,QF有最大值.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系![]() 中,直线
中,直线![]() 分别与
分别与![]() 、
、![]() 轴交于点
轴交于点![]() ,
,![]() ,与反比例函数的图象分别交于点
,与反比例函数的图象分别交于点![]() 、
、![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)求该反比例函数的解析式;
(3)连接![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下面两题中只选做一题,如果做了两题的,只按第(1)题评分:
(1)用“=>”与“<=”表示一种运算法则:(a=>b)=﹣b,(a<=b)=﹣a,如(2=>3)=﹣3,则(2010=>2011)<=(2009=>2008)=________(括号运算优先)
(2)用“>”或“<”号填空:sin40°cos50°﹣![]() ________0.(可用计算器计算)
________0.(可用计算器计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
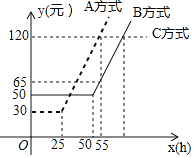
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
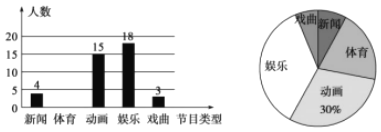
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①![]() ; ②
; ②![]() ; ③
; ③![]() ;④CE2=CD×BC; ⑤BE2=AE×BC
;④CE2=CD×BC; ⑤BE2=AE×BC

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的四个顶点都在格点上,且点A、B的坐标分别为![]() 、
、![]() 请解答下列问题:
请解答下列问题:
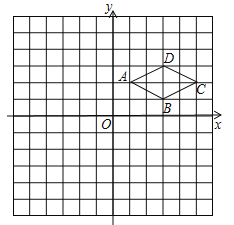
(1)写出点C、D的坐标;
(2)画出菱形ABCD关于y轴对称的四边形![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(3)画出菱形ABCD关于原点O对称的四边形![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
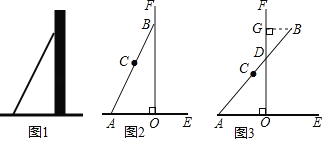
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
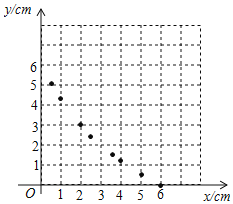
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com