
【题目】如图,在正方OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,![]() .若
.若![]() ,则点F的纵坐标是( )
,则点F的纵坐标是( )
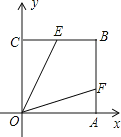
A.1B.![]() C.2D.
C.2D.![]()
【答案】B
【解析】
如图连接EF,延长BA使得AM=CE,则△OCE≌△OAM.先证明△OFE≌△FOM,推出EF=FM=AF+AM=AF+CE,设AF=x,在Rt△EFB中利用勾股定理列出方程即可解决问题.
如图连接EF,延长BA使得AM=CE,则△OCE≌△OAM.
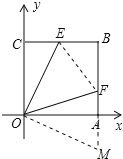
∴OE=OM,∠COE=∠MOA,
∵∠EOF=45°,
∴∠COE+∠AOF=45°,
∴∠MOA+∠AOF=45°,
∴∠EOF=∠MOF,
在△OFE和△OFM中,
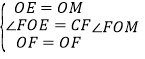 ,
,
∴△OFE≌△FOM,
∴EF=FM=AF+AM=AF+CE,设AF=x,
∵CE=![]() ,
,
∴EF=2+x,EB=2,FB=4-x,
∴(2+x)2=22+(4-x)2,
∴x=![]() ,
,
∴点F的纵坐标为![]() ,
,
故选B.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(-1,0),C(0,-5)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q. 若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
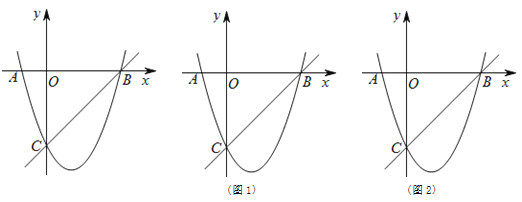
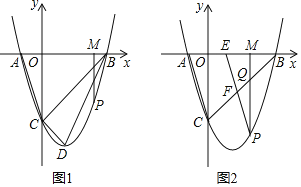
【题目】如图1,抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3),抛物线顶点为D,连接AC,BC,CD,BD,点P是x轴下方抛物线上的一个动点,作PM⊥x轴于点M,设点M的横坐标为m.
(1)求抛物线的解析式及点D的坐标;
(2)试探究是否存在这样的点P,使得以P,M,B为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图2,PM交线段BC于点Q,过点P作PE∥AC交x轴于点E,交线段BC于点F,请用含m的代数式表示线段QF的长,并求出当m为何值时QF有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
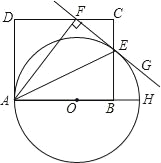
【题目】如图,AH是圆O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.
(1)求证:直线FG是⊙O的切线;
(2)若AD=8,EB=5,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴只有一个交点,以下四个结论:①抛物线的对称轴在
轴只有一个交点,以下四个结论:①抛物线的对称轴在![]() 轴左侧;②关于
轴左侧;②关于![]() 的方程
的方程![]() 有实数根;③
有实数根;③![]() ;④
;④![]() 的最大值为1.其中结论正确的为( )
的最大值为1.其中结论正确的为( )
A.①②③B.③④C.①③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 的矩形,点
的矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,直线
,直线![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
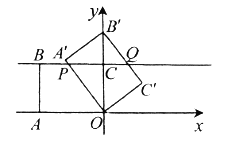
(Ⅰ)如图①,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 轴正半轴上时,
轴正半轴上时,
(1)求证:![]() ;
;
(2)求点![]() 的坐标.
的坐标.
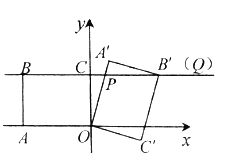
(Ⅱ)如图②,当矩形![]() 的顶点
的顶点![]() 落在直线
落在直线![]() 上时,
上时,
(1)求证:![]() .
.
(2)求点![]() 的坐标.
的坐标.
(Ⅲ)在矩形![]() 旋转过程中,当
旋转过程中,当![]() 时,若
时,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
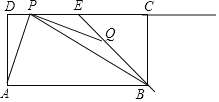
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com