
【题目】在平面直角坐标系中,四边形![]() 的矩形,点
的矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,直线
,直线![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
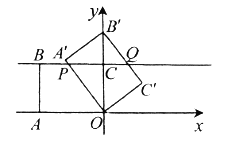
(Ⅰ)如图①,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 轴正半轴上时,
轴正半轴上时,
(1)求证:![]() ;
;
(2)求点![]() 的坐标.
的坐标.
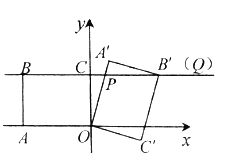
(Ⅱ)如图②,当矩形![]() 的顶点
的顶点![]() 落在直线
落在直线![]() 上时,
上时,
(1)求证:![]() .
.
(2)求点![]() 的坐标.
的坐标.
(Ⅲ)在矩形![]() 旋转过程中,当
旋转过程中,当![]() 时,若
时,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
【答案】(Ⅰ)(1)见解析;(2)点![]() 的坐标为
的坐标为![]() ; (Ⅱ)(1)见解析;(2)点
; (Ⅱ)(1)见解析;(2)点![]() 的坐标为
的坐标为![]() ;(Ⅲ)点
;(Ⅲ)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(Ⅰ)(1)由题意得∠B’CQ=∠C’即可求解;
(2)由题可得OA=8,OC=6. B’C’=BC=8,OC’=OC=6;由(1)知△B’CQ∽△B’C’O即可求解;
(Ⅱ)(1)由题意知A’B’=AB=OC,∠BCO=∠B’CO=∠A’=90,易得三角形全等;
(2)设CP=x,由(1)知△PCO≌△PA’B’,易得CP长即可求出P点坐标;
(3)分情况讨论:1°当P在BQ上时,由勾股定理易得PC长度即可求解;
2°当P在QB延长线上时,由勾股定理易得PC长度,即可求解.
(Ⅰ)(1)证明:根据题意,知∠B’CQ=∠BCO=90°,∠BCO=∠C’=90°,
∴∠B’CQ=∠C’=90°.
又∵∠QB’C=∠OB’C’
∴△B’CQ∽△B’C’O.
(2)解:∵点A(-8,0)C(0,6),∴OA=8,OC=6.
∵四边形OABC是矩形,∴BC=OA=8.
根据题意,知B’C’=BC=8,OC’=OC=6.
∴OB’=10,B’C=OB’-OC=4.
由(1)知△B’CQ∽△B’C’O,∴![]() ,即
,即![]() .∴CQ=3.
.∴CQ=3.
∴点Q的坐标为(3,6).
(Ⅱ)(1)证明:由题意知A’B’=AB=OC,∠BCO=∠B’CO=∠A’=90°,
又∵∠CPO=∠A’PB’∴ △PCO≌△PA’B’.
(2)解:根据题意,知A’O=AO=8.
设CP=x,由(1)知△PCO≌△PA’B’,
∴A’P=CP=x,A’B’=OC=6,PB’=PO=A’O-A’P=8-x.
在Rt△PA’B’中,![]() ,即
,即![]() ,
,
解得x=![]() ,∴CP=
,∴CP=![]() .
.
∴点P的坐标为(![]() ,6).
,6).
(Ⅲ)对于△PQO,PQ边上的高CO等于PO边上的高C’O
设BP=n
1°当P在BQ上时,∵BQ=2BP∴BP=PQ=n
在Rt△PCO中,由勾股定理得![]() 解得
解得![]()
∴PC=BC-BP=8-![]() =
=![]() 故P点坐标为(
故P点坐标为(![]() ,6)
,6)
2°当P在QB的延长线上时,∵BQ=2BP∴PQ= 3BP=3n
在Rt△PCO中,由勾股定理得![]() 解得
解得![]() 或
或![]() (舍)
(舍)
∴PC=BC+BP=8+![]() =
=![]() 故P点坐标为(-9-
故P点坐标为(-9-![]() ,6)
,6)
综上所述,点P的坐标为(-9-![]() ,6)或(
,6)或(![]() ,6).
,6).


科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
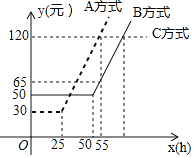
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,点
为坐标原点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 为
为![]() 轴的正半轴上一动点.以
轴的正半轴上一动点.以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() ,
,![]() ,点
,点![]() 在第一象限内.连接
在第一象限内.连接![]() ,交
,交![]() 轴于点
轴于点![]() .
.

(Ⅰ)用含![]() 的式子表示点
的式子表示点![]() 的坐标;
的坐标;
(Ⅱ)在点![]() 运动的过程中,判断
运动的过程中,判断![]() 的长是否发生变化?若不变求出其值,若变化请说明理由;
的长是否发生变化?若不变求出其值,若变化请说明理由;
(Ⅲ)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系式.
之间的数量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
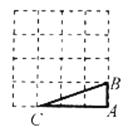
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点
放在每个小正方形的边长为1的网格中,点![]() ,点
,点![]() ,点
,点![]() 均落在格点上.
均落在格点上.
(Ⅰ)![]() 的长等于______________________.
的长等于______________________.
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出![]() 关于直线
关于直线![]() 对称的图形,并简要说明画图方法(不要求证明).
对称的图形,并简要说明画图方法(不要求证明).
________________________________________________________________________________________________________________________________________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
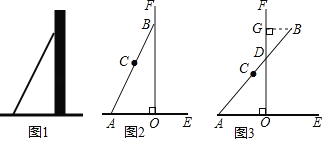
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
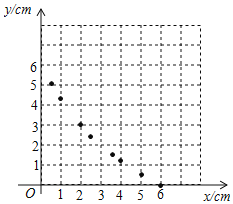
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
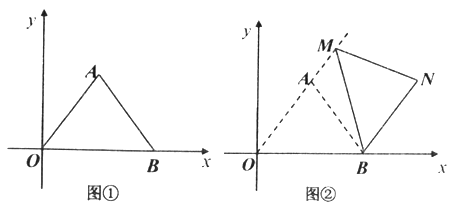
(Ⅰ)如图①,求AB的长;
(Ⅱ)如图②,把图①中的![]() 绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
①求证:![]() ;②求点N的坐标;
;②求点N的坐标;
(Ⅲ)点C是OB的中点,点D为线段OA上的动点,在![]() 绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,交x轴于
,交x轴于![]() ,交y轴的负半轴于点C,顶点为D.
,交y轴的负半轴于点C,顶点为D.

有下列结论:
①![]()
②![]() ;
;
③当△ABD是等腰直角三角形时,则![]() ;
;
④当△ABC是等腰三角形时,a的值有3个,其中,正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com