
【题目】如图,抛物线![]() ,交x轴于
,交x轴于![]() ,交y轴的负半轴于点C,顶点为D.
,交y轴的负半轴于点C,顶点为D.

有下列结论:
①![]()
②![]() ;
;
③当△ABD是等腰直角三角形时,则![]() ;
;
④当△ABC是等腰三角形时,a的值有3个,其中,正确结论的个数是( )
A. 1B. 2C. 3D. 4
【答案】B
【解析】
根据![]() 的交点是
的交点是![]() ,可知对称轴为x=1,从而可判断①;根据①的结论及a-b+c=0可得c与a的关系,从而判断②;当△ABD是等腰直角三角形时,可知D(1,-2)代入二次函数解析式,结合b=-2a,c=-3a判断③;根据等腰三角形的变得关系判断C点的个数,从而判断④.
,可知对称轴为x=1,从而可判断①;根据①的结论及a-b+c=0可得c与a的关系,从而判断②;当△ABD是等腰直角三角形时,可知D(1,-2)代入二次函数解析式,结合b=-2a,c=-3a判断③;根据等腰三角形的变得关系判断C点的个数,从而判断④.
∵![]() 的交点是
的交点是![]() ,
,
∴对称轴为:x=1,
∴![]()
∴b=-2a,即,故![]() ①正确;
①正确;
∵(-1,0)在二次函数的图象上,
∴a-b+c=0,
∴c=-3a,
又∵a>0
∴2c=3b,故②错误;
当△ABD是等腰直角三角形时,
则D(1,-2)代入二次函数解析式,
又∵b=-2a,c=-3a,
即a-2a-3a=-2,∴![]() ,故③正确;
,故③正确;
当△ABC是等腰三角形时,当AB=AC或AB=BC,
则满足条件的C有两种可能,AC=BC不存在,故④错误,
故选B.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 的矩形,点
的矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,直线
,直线![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
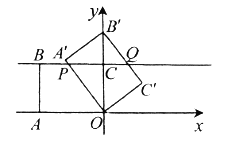
(Ⅰ)如图①,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 轴正半轴上时,
轴正半轴上时,
(1)求证:![]() ;
;
(2)求点![]() 的坐标.
的坐标.
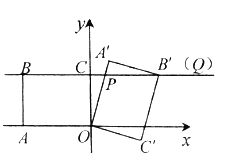
(Ⅱ)如图②,当矩形![]() 的顶点
的顶点![]() 落在直线
落在直线![]() 上时,
上时,
(1)求证:![]() .
.
(2)求点![]() 的坐标.
的坐标.
(Ⅲ)在矩形![]() 旋转过程中,当
旋转过程中,当![]() 时,若
时,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
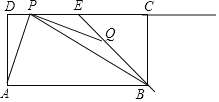
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
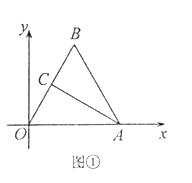
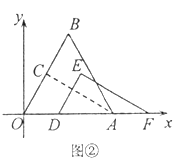
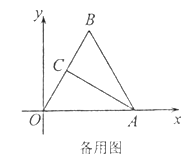
【题目】在平面直角坐标系中,点A(4,0),B为第一象限内一点,且![]() 为等边三角形,C为OB的中点,连接AC.
为等边三角形,C为OB的中点,连接AC.
(I)如图①,求点C的坐标;
(I)如图②,将![]() 沿x轴向右平移得到
沿x轴向右平移得到![]() ,设
,设![]() ,其中
,其中![]()
①设![]() 与
与![]() 重叠部分的面积为S,用含m的式子表示S:
重叠部分的面积为S,用含m的式子表示S:
②连接![]() ,当
,当![]() 取最小值时,求点E的坐标(直接写出结果即可).
取最小值时,求点E的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在紧张的中考复习之际,为确保学生的饮食健康与安全,部分家长组织成立中考护卫小分队,每天不辞辛劳从城区进购正规检疫菜品。某甲、乙两种菜品每份进价分别为 14 元、16 元,售价均为每份 18 元,这两种菜品每天的进价总额为 1480 元,全部销售完每天总利润为 320 元.
(1)该甲、乙两种菜品每天各卖出多少份?
(2)因受气温变化的影响,甲种菜品进价每份上涨 a 0 a 4元,为确保学生的营养,在每天两种菜品的进购总量不变的情况下,要求甲种菜品的数量不得低于 10 份,也不超过乙种菜品的 3 倍,则进购甲种菜品多少份才能使每天的总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
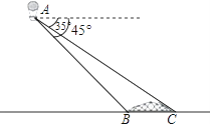
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
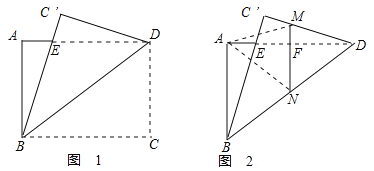
【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
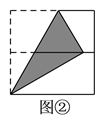
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
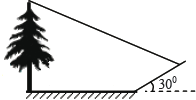
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com