
【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
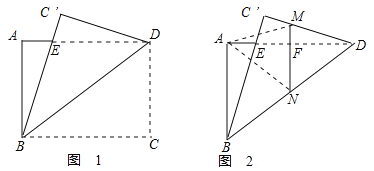
【答案】![]()
【解析】
由折叠的性质可知△DFM为直角三角形,且DF=![]() AD=2,可证△ABE≌△
AD=2,可证△ABE≌△![]() DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
解:如图,由已知可得MN垂直平分AD,DF=![]() AD=2,FN=
AD=2,FN=![]() AB=
AB=![]() ,
,
∵AB=CD=![]() D,∠A=∠
D,∠A=∠![]() =90°,∠AEB=∠
=90°,∠AEB=∠![]() ED,
ED,
∴△ABE≌△![]() DE,∴BE=ED, ∠ABE=∠
DE,∴BE=ED, ∠ABE=∠![]() DE
DE
设AE=x,则BE=ED=4-x,
在Rt△ABE中,由勾股定理得
AB2+AE2=BE2,即32+x2=(4-x)2,
解得x=![]() ,∴AE=
,∴AE=![]()
∵∠ABE=∠![]() DE, ∠BAE=∠
DE, ∠BAE=∠![]() =90°,
=90°,
∴△ABE∽△FDM,
∴![]() =
=![]() ,即
,即  ,
,
解得MF=![]() .
.
∴MN=NF+FM=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
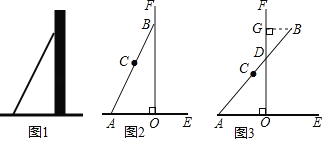
【题目】数学活动课上,张老师引导同学进行如下探究:如图1,将长为![]() 的铅笔
的铅笔![]() 斜靠在垂直于水平桌面
斜靠在垂直于水平桌面![]() 的直尺
的直尺![]() 的边沿上,一端
的边沿上,一端![]() 固定在桌面上,图2是示意图.
固定在桌面上,图2是示意图.
活动一
如图3,将铅笔![]() 绕端点
绕端点![]() 顺时针旋转,
顺时针旋转,![]() 与
与![]() 交于点
交于点![]() ,当旋转至水平位置时,铅笔
,当旋转至水平位置时,铅笔![]() 的中点
的中点![]() 与点
与点![]() 重合.
重合.
数学思考
(1)设![]() ,点
,点![]() 到
到![]() 的距离
的距离![]() .
.
①用含![]() 的代数式表示:
的代数式表示:![]() 的长是_________
的长是_________![]() ,
,![]() 的长是________
的长是________![]() ;
;
②![]() 与
与![]() 的函数关系式是_____________,自变量
的函数关系式是_____________,自变量![]() 的取值范围是____________.
的取值范围是____________.
活动二
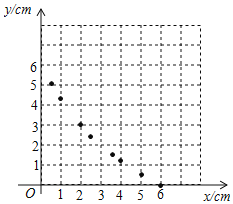
(2)①列表:根据(1)中所求函数关系式计算并补全表格.
| 6 | 5 | 4 | 3.5 | 3 | 2.5 | 2 | 1 | 0.5 | 0 |
| 0 | 0.55 | 1.2 | 1.58 | 1.0 | 2.47 | 3 | 4.29 | 5.08 |
②描点:根据表中数值,描出①中剩余的两个点![]() .
.
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考
(3)请你结合函数的图象,写出该函数的两条性质或结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将![]() 放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
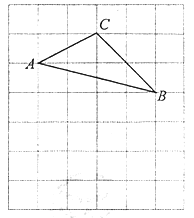
(I)计算![]() 的值等于____________;
的值等于____________;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边、面积等于![]() 的矩形,并简要说明画图方法(不要求证明)_____________.
的矩形,并简要说明画图方法(不要求证明)_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,交x轴于
,交x轴于![]() ,交y轴的负半轴于点C,顶点为D.
,交y轴的负半轴于点C,顶点为D.

有下列结论:
①![]()
②![]() ;
;
③当△ABD是等腰直角三角形时,则![]() ;
;
④当△ABC是等腰三角形时,a的值有3个,其中,正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知抛物线![]() 与x轴交于A,B两点(点d在点B的右侧),与y轴交于点
与x轴交于A,B两点(点d在点B的右侧),与y轴交于点![]() ,顶点为D.
,顶点为D.
(I)求该抛物线的解析式及顶点D的坐标:
(Ⅱ)Q为线段BD上一点,点A关于∠AQB的平分线的对称点为A',
①判断点A'与直线BQ的位置关系:点![]() (填写“在”或“不在”)直线BQ上:
(填写“在”或“不在”)直线BQ上:
②若![]() ,求点2的坐标:
,求点2的坐标:
(Ⅲ)若此抛物线的对称轴上的点P满足![]() ,求点P的坐标。
,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有600名学生,在体育中考前进行了一次模拟体测.从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
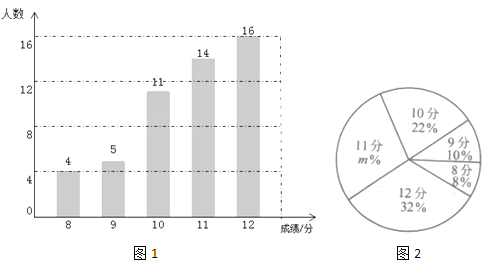
(Ⅰ)本次抽取到的学生人数为 ,图2中![]() 的值为 ;
的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]()
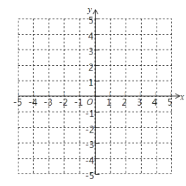
(1)将其配方成顶点式,并写出它的图象的开口方向、顶点坐标、对称轴.
(2)在如图所示的直角坐标系中画出函数图象,并指出当y<0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
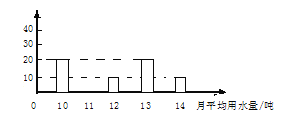
【题目】为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况做一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨)并将调查结果制成了如图所示的条形统计图。
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
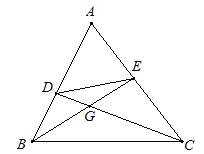
【题目】已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE =∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com