
【题目】为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况做一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨)并将调查结果制成了如图所示的条形统计图。
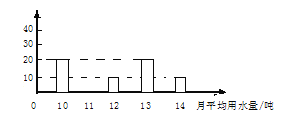
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中平均用水量不超过12吨的约有多少户?
【答案】(1)补全图形见解析; (2)平均数11.6吨,众数11,中位数11;(3)350户.
【解析】试题分析:(1)根据条形图中数据得出平均用水11吨的户数,进而画出条形图即可;(2)根据平均数、中位数、众的定义分别求解即可;(3)根据样本估计总体得出答案即可.
试题解析: (1)根据条形图可得出:
平均用水11吨的用户为:10020102010=40(户),
如图所示:
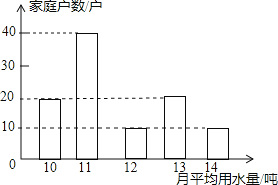
(2)平均数为:![]() (20×10+40×11+12×10+13×20+10×14)=11.6(吨),
(20×10+40×11+12×10+13×20+10×14)=11.6(吨),
根据11出现次数最多,故众数为:11,
根据100个数据的最中间为第50和第51个数据,
按大小排列后第50,51个数据是11,故中位数为:11;
答:这100个样本数据的平均数,众数和中位数分别是11.6,11,11;
(3)样本中不超过12吨的有20+40+10=70(户),
所以黄冈市直机关500户家庭中月平均用水量不超过12吨的约有500×![]() =350户.
=350户.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
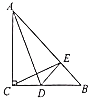
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,折叠
的平分线,折叠![]() 使得点
使得点![]() 落在
落在![]() 边上的
边上的![]() 处,连接
处,连接![]() 、
、![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 是等腰三角形;③
是等腰三角形;③![]() ;④
;④![]() .其中正确的结论是______.(填写序号)
.其中正确的结论是______.(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系内,已知点P(3,3),A(0,b)是y轴上一点,过P作PA的垂线交x轴于B(a,0),则称Q(a,b)为点P的一个关联点。
(1)写出点P的不同的两个关联点的坐标是 、 ;
(2)若点P的关联点Q(x,y)满足5x-3y=14,求出Q点坐标;

(3)已知C(-1,-1)。若点A、点B均在所在坐标轴的正半轴上运动,求△CAB的面积最大值,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com