
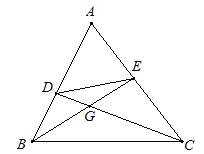
【题目】已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE =∠ACD,BE、CD交于点G.
(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题(1)先证△ABE∽△ACD,得出![]() ,再利用∠A是公共角,即可求证;(2)在BC上截取BF=BD,连接EF,先证△BDE≌△BFE,得出DE=FE,∠BDE=∠BFE,再证EF=EC即可.
,再利用∠A是公共角,即可求证;(2)在BC上截取BF=BD,连接EF,先证△BDE≌△BFE,得出DE=FE,∠BDE=∠BFE,再证EF=EC即可.
解:(1)∵∠ABE =∠ACD,且∠A是公共角,
∴△ABE∽△ACD.
∴![]() ,即
,即![]() ,
,
又∵∠A是公共角,
∴△AED∽△ABC.
(2)在BC上截取BF=BD,连接EF,
在△BDE与△BFE中,BD=BF,∠DBE=∠FBE,BE=BE,
∴△BDE≌△BFE,
∴DE=FE,∠BDE=∠BFE,∴∠ADE=∠EFC,
∵△AED∽△ABC,∴∠ADE=∠ACB,
∴∠EFC=∠ACB,
∴EF=EC,
∴DE=CE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
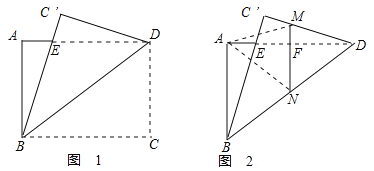
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
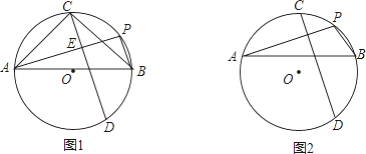
【题目】(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为![]() 的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧![]() 的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
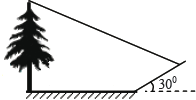
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
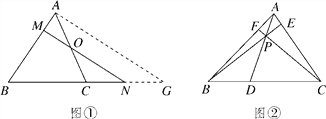
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
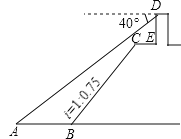
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
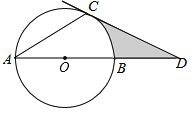
(1)求证:AC=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com