
【题目】已知二次函数y=![]()
(1)将其配方成顶点式,并写出它的图象的开口方向、顶点坐标、对称轴.
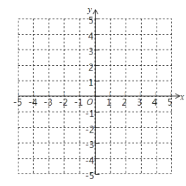
(2)在如图所示的直角坐标系中画出函数图象,并指出当y<0时x的取值范围.
科目:初中数学 来源: 题型:
【题目】在紧张的中考复习之际,为确保学生的饮食健康与安全,部分家长组织成立中考护卫小分队,每天不辞辛劳从城区进购正规检疫菜品。某甲、乙两种菜品每份进价分别为 14 元、16 元,售价均为每份 18 元,这两种菜品每天的进价总额为 1480 元,全部销售完每天总利润为 320 元.
(1)该甲、乙两种菜品每天各卖出多少份?
(2)因受气温变化的影响,甲种菜品进价每份上涨 a 0 a 4元,为确保学生的营养,在每天两种菜品的进购总量不变的情况下,要求甲种菜品的数量不得低于 10 份,也不超过乙种菜品的 3 倍,则进购甲种菜品多少份才能使每天的总利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
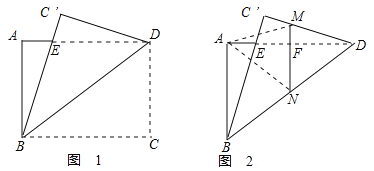
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1)(x+1)2﹣4=0;
(2)12(2﹣x)2﹣9=0;
(3)x(3x+2)﹣6(3x+2)=0
(4)(x+2)2﹣16=0;
(5)(2x+3)2﹣25=0;
(6)4(1﹣3x)2=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
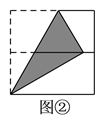
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
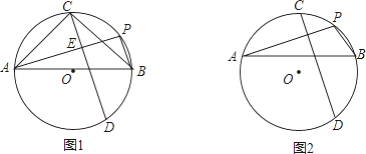
【题目】(1)如图1,PA、PB是⊙O的两条弦,AB为直径,C为![]() 的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
的中点,弦CD⊥PA于点E,写出AB与AC的数量关系,并证明;
(2)如图2,PA、PB是⊙O的两条弦,AB为弦,C为劣弧![]() 的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
的中点,弦CD⊥PA于E,写出AE、PE与PB的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com