练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,在平面直角坐标系xOy中,菱形ABCD的四个顶点都在格点上,且点A、B的坐标分别为、请解答下列问题:

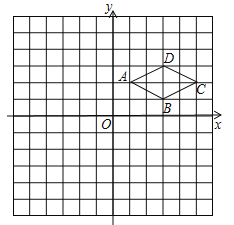
    (1)写出点C、D的坐标;

    (2)画出菱形ABCD关于y轴对称的四边形,并写出点的坐标;

    (3)画出菱形ABCD关于原点O对称的四边形,并写出点的坐标.

    【答案】（1）C(5，2）， D（3，3）；(2)见解析；（3）见解析.

    【解析】

    （1）根据图象即可得到结论；

    （2）根据关于y轴对称的点的坐标特点画出四边形A1B1C1D1即可；

    （3）根据关于原点O对称的点的坐标特点即可得到四边形ABCD关于原点O对称的四边形A2B2C2D2．

    （1）C（5，2），D（3，3）；

    （2）如图所示，四边形A1B1C1D1即为所求；A1（-1，2）；

    （3）如图所示，四边形A2B2C2D2即为所求；B2（-3，-1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小琴的父母承包了一块荒山地种植一批梨树，今年收获一批金溪密梨，小琴的父母打算以m元/斤的零售价销售5000斤密梨；剩余的5000(m＋1)斤密犁以比零售价低1元的批发价批给外地客商，预计总共可赚得55 000元的毛利润．

    （1）求小琴的父母今年共收获金溪密梨多少斤？

    （2）若零售金溪密梨平均每天可售出200斤，每斤盈利2元．为了加快销售和获得较好的售价，采取了降价措施，发现销售单价每降低0.1元，平均每天可多售出40斤，应降价多少元？每天销售利润为600元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

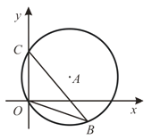
    【题目】如图，直径为10的⊙A经过点C(0,5)和点O (0,0)，B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为 _________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

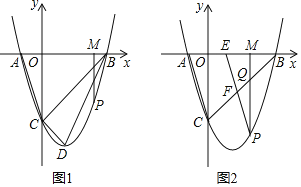
    【题目】如图1，抛物线与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C（0，﹣3），抛物线顶点为D，连接AC，BC，CD，BD，点P是x轴下方抛物线上的一个动点，作PM⊥x轴于点M，设点M的横坐标为m．

    （1）求抛物线的解析式及点D的坐标；

    （2）试探究是否存在这样的点P，使得以P，M，B为顶点的三角形与△BCD相似？若存在，请求出点P的坐标；若不存在，请说明理由；

    （3）如图2，PM交线段BC于点Q，过点P作PE∥AC交x轴于点E，交线段BC于点F，请用含m的代数式表示线段QF的长，并求出当m为何值时QF有最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．

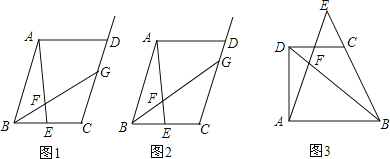
    原题：如图1，在ABCD中，点E是BC边上的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若=3，求的值．

    （1）尝试探究

    在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是 ，CG和EH的数量关系是 ，的值是

    （2）类比延伸

    如图2，在原题的条件下，若=m（m≠0），则的值是 （用含m的代数式表示），试写出解答过程．

    （3）拓展迁移

    如图3，梯形ABCD中，DC∥AB，点E是BC延长线上一点，AE和BD相交于点F，若=a，=b（a＞0，b＞0），则的值是 （用含a，b的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛，在选拔比赛中，每人射击10次，他们10次成绩的平均数及方差如下表所示：

    甲

    乙

    丙

    丁

    平均数/环

    9.5

    9.5

    9.6

    9.6

    方差/环2

    5.1

    4.7

    4.5

    5.1

    请你根据表中数据选一人参加比赛，最合适的人选是(　 　)

    A. 甲 B. 乙 C. 丙 D. 丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

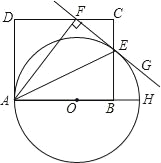
    【题目】如图，AH是圆O的直径，AE平分∠FAH，交⊙O于点E，过点E的直线FG⊥AF，垂足为F，B为直径OH上一点，点E、F分别在矩形ABCD的边BC和CD上．

    （1）求证：直线FG是⊙O的切线；

    （2）若AD=8，EB=5，求⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与轴只有一个交点，以下四个结论：①抛物线的对称轴在轴左侧；②关于的方程有实数根；③；④的最大值为1.其中结论正确的为（ ）

    A.①②③B.③④C.①③D.①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边中，D是BC延长线上一点，，E，F分别是BC，AD的中点，若，则线段EF的长是____.

    查看答案和解析>>

    同步练习册答案