
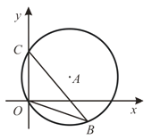
【题目】如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为 _________________.
科目:初中数学 来源: 题型:
【题目】去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩( | 频数(人数) |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
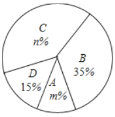
根据以上信息,解答以下问题:
(1)表中的![]() ;
;
(2)扇形统计图中![]() ,
,![]() ,
,![]() 等级对应的扇形的圆心角为 度;
等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得![]() 等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用
等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用![]() ,
,![]() ,
,![]() 表示)和3名女生(用
表示)和3名女生(用![]() ,
,![]() ,
,![]() 表示),请用列表或画树状图的方法求恰好选取的是
表示),请用列表或画树状图的方法求恰好选取的是![]() 和
和![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
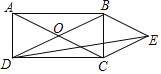
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,AB:BC=2:1,且BE∥AC,CE∥DB,连接DE,则tan∠EDC=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在( )
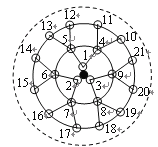
A.第3天B.第4天C.第5天D.第6天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年五月,我国南方某省A、B两市遭受严重洪涝灾害,邻近县市C、D决定调运物资支援A、B两市灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)A、B两市各需救灾物资多少吨?
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四种活动形式:A:跑步;B:跳绳;C:做操;D:游戏,全校学生都选择了一种形式参与活动,小明对同学们选择的活动形式进行了随机抽样调查,并绘制了不完整的两幅统计图(如图):
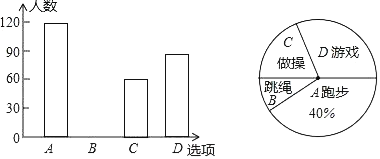
(1)本次共调查了多少名学生?
(2)跳绳B对应扇形的圆心角为多少度?
(3)学校在每班A、B、C、D四种活动形式中,随机抽取两种开展活动,求每班抽取的两种形式恰好是“做操”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
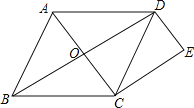
【题目】如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形OCED是矩形.
(2)若AB=4,∠ABC=60°,求矩形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
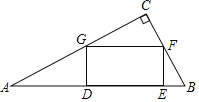
【题目】如图,在△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上,设AG=5,AD=4,求△ADG与△FEB的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+b与双曲线![]() 交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线
交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线![]() 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线![]() 于点N.
于点N.
(1)当点A的横坐标为1时,求b的值:
(2)在(1)的条件下,设P点的横坐标为m,
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com