
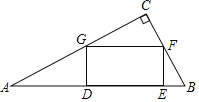
【题目】如图,在△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上,设AG=5,AD=4,求△ADG与△FEB的面积比.
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数 y=f(x)满足:对于自变量 x 的取值范围内的任意 x1,x2,
(1)若 x1<x2,都有 f(x1)<f(x2),则称 f(x)是增函数;
(2)若 x1<x2,都有 f(x1)>f(x2),则称 f(x)是减函数.
例题:证明函数f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
证明:设 0<x1<x2,
f(x1)﹣f(x2)=![]() .
.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴![]() >0.即 f(x1)﹣f(x2)>0.
>0.即 f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数 f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数![]() .
.
f(﹣1)=![]() +(﹣2)=-1,f(﹣2)=
+(﹣2)=-1,f(﹣2)=![]() +(﹣4)=
+(﹣4)=![]() .
.
(1)计算:f(﹣3)= ,f(﹣4)= ;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
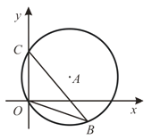
【题目】如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为 _________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
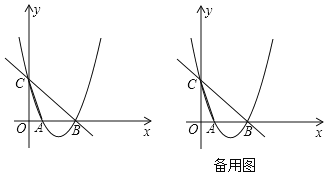
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与x轴交于点B,与y轴交于点C.抛物线y=x2+bx+c经过点B和点C,与x轴交于另一点A,连接AC.
(1)求抛物线的解析式;
(2)若点Q在直线BC上方的抛物线上,连接QC,QB,当△ABC与△QBC的面积比等于2:3时,直接写出点Q的坐标:
(3)在(2)的条件下,点H在x轴的负半轴,连接AQ,QH,当∠AQH=∠ACB时,直接写出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
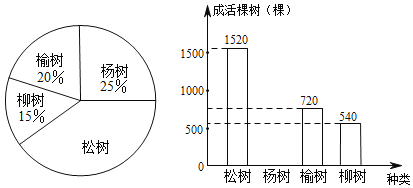
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块宣传牌![]() .小明在山坡的坡脚
.小明在山坡的坡脚![]() 处测得宣传牌底部
处测得宣传牌底部![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处测得宣传牌顶部
处测得宣传牌顶部![]() 的仰角为
的仰角为![]() .已知山坡
.已知山坡![]() 的坡度
的坡度![]() ,
,![]() 米,
米,![]() 米.
米.
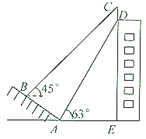
(1)求点![]() 距地面的高度;
距地面的高度;
(2)求大楼![]() 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
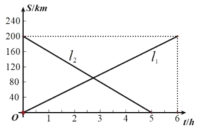
【题目】已知![]() 两地相距
两地相距![]() ,甲、乙两辆货车装满货物分别从
,甲、乙两辆货车装满货物分别从![]() 两地相向而行,图中
两地相向而行,图中![]() 分别表示甲、乙两辆货车离
分别表示甲、乙两辆货车离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数关系.请你根据以上信息,解答下列问题:
之间的函数关系.请你根据以上信息,解答下列问题:
(1)分别求出直线![]() 所对应的函数关系式;
所对应的函数关系式;
(2)何时甲货车离![]() 地的距离大于乙货车离
地的距离大于乙货车离![]() 地的距离?
地的距离?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击疫情,我们每个人都要做到讲卫生,勤洗手,科学消毒,如图(1)是一瓶消毒洗手液. 图(2)是它的示意图,当手按住顶部A下压时,洗手液瞬间从喷口B流出,路线从抛物线经过C,E两点.瓶子上部分是由弧![]() 和弧
和弧![]() 组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,CG=8 cm,GH=10 cm,点E到台面GH的距离为14 cm,点B到台面的距离为20 cm,且B,D,H三点共线.若手心距DH的水平距离为2 cm时刚好接洗手液,此时手心距水平台面的高度为______cm.
组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,CG=8 cm,GH=10 cm,点E到台面GH的距离为14 cm,点B到台面的距离为20 cm,且B,D,H三点共线.若手心距DH的水平距离为2 cm时刚好接洗手液,此时手心距水平台面的高度为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
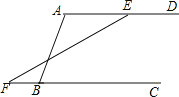
【题目】如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°
,tan72°![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com