
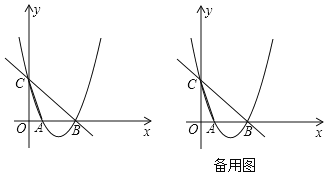
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与x轴交于点B,与y轴交于点C.抛物线y=x2+bx+c经过点B和点C,与x轴交于另一点A,连接AC.
(1)求抛物线的解析式;
(2)若点Q在直线BC上方的抛物线上,连接QC,QB,当△ABC与△QBC的面积比等于2:3时,直接写出点Q的坐标:
(3)在(2)的条件下,点H在x轴的负半轴,连接AQ,QH,当∠AQH=∠ACB时,直接写出点H的坐标.
【答案】(1)y=x2﹣6x+5;(2)点Q(﹣1,12)或(6,5);(3)点H的坐标为:(﹣19,0)或(﹣![]() ,0).
,0).
【解析】
(1)直线y=-x+5与x轴交于点B,与y轴交于点C,则点B、C的坐标分别为:(5,0)、(0,5),即可求解;
(2)过点A作直线BC的平行线n交y轴于点M,则点M(0,1),则CM=5-1=4,在点C上方取CN=![]() CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,即可求解
CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,即可求解
(3)分点Q(6,5)、点Q(-1,12)两种情况,分别求解即可.
解:(1)直线y=﹣x+5与x轴交于点B,与y轴交于点C,则点B、C的坐标分别为:(5,0)、(0,5),则c=5,将点B的坐标代入抛物线表达式并解得:b=﹣6,
故抛物线的表达式为:y=x2﹣6x+5;
(2)过点A作直线BC的平行线n交y轴于点M,则点M(0,1),则CM=5﹣1=4,
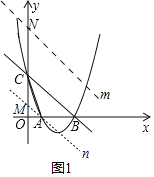
在点C上方取CN=![]() CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,
CM=6,过点N作直线m交抛物线于点Q(Q′),则点Q为所求,
则点N(0,11),则直线m的表达式为:y=﹣x+11…②,
联立①②并解得:x=﹣1或6,
故点Q(﹣1,12)或(6,5);
(3)过点A作AK⊥BC于点K,
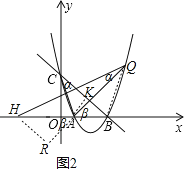
AB=4,则AK=BK=![]() ,AC=
,AC=![]() ,
,
则sin∠ABC=![]() =sinα,则tanα=
=sinα,则tanα=![]() ;
;
①当点Q(6,5)时,
过点H作HR⊥AQ交QA的延长线于点R
由点A、Q的坐标知,tan∠QAB=1=tanβ,故β=45°,AQ=5![]() ,
,
则HR=AR=x,tan∠HQR=tanα=![]() ,
,
解得:x=10![]() ,AH=
,AH=![]() x=20,
x=20,
故点H(﹣19,0);
②当点Q(﹣1,12)时,
同理可得:点H(﹣![]() ,0);
,0);
综上,点H的坐标为:(﹣19,0)或(﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
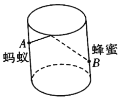
【题目】如图,圆柱形玻璃杯高为![]() ,底面周长为
,底面周长为![]() ,在杯内壁离杯底
,在杯内壁离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁上,它在离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁上,它在离杯上沿![]() 且与蜂蜜相对的
且与蜂蜜相对的![]() 处,则蚂蚁从外壁
处,则蚂蚁从外壁![]() 处走到内壁
处走到内壁![]() 处,至少爬多少厘米才能吃到蜂蜜( )
处,至少爬多少厘米才能吃到蜂蜜( )
A.24B.25C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在( )
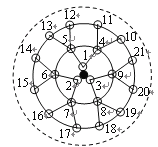
A.第3天B.第4天C.第5天D.第6天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四种活动形式:A:跑步;B:跳绳;C:做操;D:游戏,全校学生都选择了一种形式参与活动,小明对同学们选择的活动形式进行了随机抽样调查,并绘制了不完整的两幅统计图(如图):
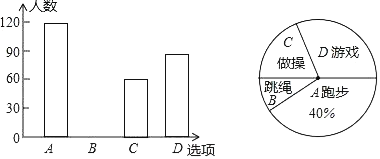
(1)本次共调查了多少名学生?
(2)跳绳B对应扇形的圆心角为多少度?
(3)学校在每班A、B、C、D四种活动形式中,随机抽取两种开展活动,求每班抽取的两种形式恰好是“做操”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
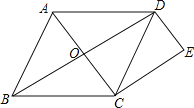
【题目】如图,点O是菱形ABCD对角线的交点,过点C作CE∥OD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形OCED是矩形.
(2)若AB=4,∠ABC=60°,求矩形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
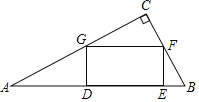
【题目】如图,在△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上,设AG=5,AD=4,求△ADG与△FEB的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将大小两把含30°角的直角三角尺按如图1 位置摆放,即大小直角三角尺的直角顶点C 重合,小三角尺的顶点 D、E 分别在大三角尺的直角边 AC、BC 上,此时小三角尺的斜边 DE 恰好经过大三角尺的重心G .已知A CDE 30°, AB 12 .
(1)求小三角尺的直角边CD 的长;
(2)将小三角尺绕点C 逆时针旋转,当点D第一次落在大三角尺的边 AB 上时(如图2),求点 B 、 E 之间的距离;
(3)在小三角尺绕点C 旋转的过程中,当直线 DE 经过点 A 时,求BAE 的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
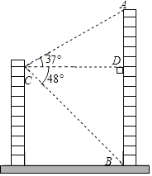
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com