
【题目】如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点C,交OB于点D,若OA=4,则阴影部分的面积为_____.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某蔬菜市场为指导某种蔬菜的生产和销售,对往年的市场行情和生产情况进行了调查,提供的信息如下:
信息1:售价和月份满足一次函数关系,如下表所示.
月份 | … | 3 | 6 | … |
售价 | … | 5 | 3 | … |
信息2:成本和月份满足二次函数关系,并且知道该种蔬菜在6月成本达到最低为1元/千克,9月成本为4元/千克.
根据以上信息回答下列问题:
(1)在7月,这种蔬菜的成本是多少元每千克?
(2)在过去的一年中,某商家平均每天卖出![]() 该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
该种蔬菜,则哪个月的利润最大,最大利润为多少?(一个月按30天计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在每个小正方形的边长为1的网格中,△ABC的顶点A、B、C均在格点上,点D为AC边上的一点.
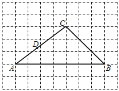
(1)线段AC的长为 .
(2)在如图所示的网格中,AM是△ABC的角平分线,在AM上求一点P,使CP+DP的值最小,请用无刻度的直尺,画出AM和点P,并简要说明AM和点P的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
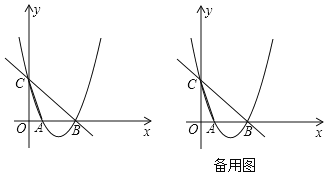
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与x轴交于点B,与y轴交于点C.抛物线y=x2+bx+c经过点B和点C,与x轴交于另一点A,连接AC.
(1)求抛物线的解析式;
(2)若点Q在直线BC上方的抛物线上,连接QC,QB,当△ABC与△QBC的面积比等于2:3时,直接写出点Q的坐标:
(3)在(2)的条件下,点H在x轴的负半轴,连接AQ,QH,当∠AQH=∠ACB时,直接写出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台![]() 型电脑和
型电脑和![]() 型打印机.如果购买1台
型打印机.如果购买1台![]() 型电脑,2台
型电脑,2台![]() 型打印机,一共需要花费6200元;如果购买2台
型打印机,一共需要花费6200元;如果购买2台![]() 型电脑,1台
型电脑,1台![]() 型打印机,一共需要花费7900元.
型打印机,一共需要花费7900元.
(1)求每台![]() 型电脑和每台
型电脑和每台![]() 型打印机的价格分别是多少元?
型打印机的价格分别是多少元?
(2)如果学校购买![]() 型电脑和
型电脑和![]() 型打印机的预算费用不超过20000元,并且购买
型打印机的预算费用不超过20000元,并且购买![]() 型打印机的台数要比购买
型打印机的台数要比购买![]() 型电脑的台数多1台,那么该学校至多能购买多少台
型电脑的台数多1台,那么该学校至多能购买多少台![]() 型打印机?
型打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块宣传牌![]() .小明在山坡的坡脚
.小明在山坡的坡脚![]() 处测得宣传牌底部
处测得宣传牌底部![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处测得宣传牌顶部
处测得宣传牌顶部![]() 的仰角为
的仰角为![]() .已知山坡
.已知山坡![]() 的坡度
的坡度![]() ,
,![]() 米,
米,![]() 米.
米.
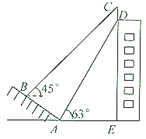
(1)求点![]() 距地面的高度;
距地面的高度;
(2)求大楼![]() 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 所有矩形都是相似的
B. 若线段a=5cm,b=2cm,则a:b=5:2
C. 若线段AB=![]() cm,C是线段AB的黄金分割点,且AC>BC,则AC=
cm,C是线段AB的黄金分割点,且AC>BC,则AC=![]() cm
cm
D. 四条长度依次为lcm,2cm,2cm,4cm的线段是成比例线段
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com