
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
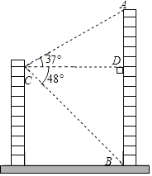
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
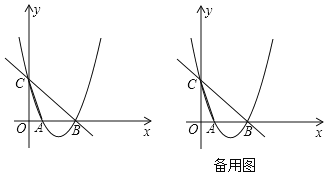
【题目】如图,在平面直角坐标系中,直线y=﹣x+5与x轴交于点B,与y轴交于点C.抛物线y=x2+bx+c经过点B和点C,与x轴交于另一点A,连接AC.
(1)求抛物线的解析式;
(2)若点Q在直线BC上方的抛物线上,连接QC,QB,当△ABC与△QBC的面积比等于2:3时,直接写出点Q的坐标:
(3)在(2)的条件下,点H在x轴的负半轴,连接AQ,QH,当∠AQH=∠ACB时,直接写出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击疫情,我们每个人都要做到讲卫生,勤洗手,科学消毒,如图(1)是一瓶消毒洗手液. 图(2)是它的示意图,当手按住顶部A下压时,洗手液瞬间从喷口B流出,路线从抛物线经过C,E两点.瓶子上部分是由弧![]() 和弧
和弧![]() 组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,CG=8 cm,GH=10 cm,点E到台面GH的距离为14 cm,点B到台面的距离为20 cm,且B,D,H三点共线.若手心距DH的水平距离为2 cm时刚好接洗手液,此时手心距水平台面的高度为______cm.
组成,其圆心分别为D,C.下部分的是矩形CGHD的视图,CG=8 cm,GH=10 cm,点E到台面GH的距离为14 cm,点B到台面的距离为20 cm,且B,D,H三点共线.若手心距DH的水平距离为2 cm时刚好接洗手液,此时手心距水平台面的高度为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海市为了增强居民的节水意识,避免水资源的浪费,全面实施居民“阶梯水价”.当累计水量达到年度阶梯水量分档基数临界点后,即开始实施阶梯价格计价,分档水量和价格见下表.
分档 | 户年用水量 (立方米) | 自来水价格 (元/立方米) | 污水处理费 (元/立方米) |
第一阶梯 | 0-220(含220) | 1.92 | 1.70 |
第二阶梯 | 220-300(含300) | 3.30 | 1.70 |
第三阶梯 | 300以上 | 4.30 | 1.70 |
注:1.应缴纳水费 = 自来水费总额 + 污水处理费总额 2.应缴纳污水处理费总额 = 用水量×污水处理费× 0.9 | |||
仔细阅读上述材料,请解答下面的问题,并把答案写在答题纸上:
(1)小静家2019年上半年共计用水量100立方米,应缴纳水费 元;
(2)小静家全年缴纳的水费共计1000.5元,那么2019年全年用水量为 立方米;
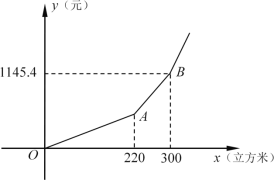
(3)如图所示是上海市“阶梯水价”y与用水量x的函数关系,那么第二阶梯(线段AB)的函数解析式为 ,定义域 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于两个不相等的实数a,b,我们规定符号max{a,b}表示a、b中的较大的数,如:max{2,4}=4,按照这个规定,方程max{x,﹣x}=x2﹣x﹣1的解为( )
A.1+![]() 或1﹣
或1﹣![]() B.1或﹣1C.1﹣
B.1或﹣1C.1﹣![]() 或1D.1+
或1D.1+![]() 或﹣1
或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
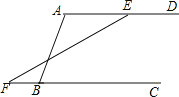
【题目】如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°
,tan72°![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解班级学生数学课前预习的具体情况,郑老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(2)扇形统计图中“课前预习不达标”对应的圆心角度数是 ;
(3)为了共同进步,郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
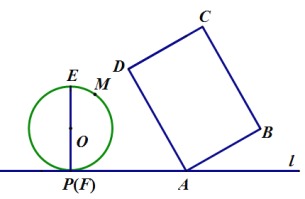
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() 与直线
与直线![]() 相交所得的锐角为
相交所得的锐角为![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() ,垂足为点
,垂足为点![]() ,与点
,与点![]() 重合,
重合,![]() ,以
,以![]() 为直径,在
为直径,在![]() 的右侧作半圆
的右侧作半圆![]() ,点
,点![]() 是半圆
是半圆![]() 上任意一点.
上任意一点.
(1)发现:连接![]() ,则线段
,则线段![]() 的最大值为____________;
的最大值为____________;
(2)矩形![]() 保持不动,半圆
保持不动,半圆![]() 沿直线
沿直线![]() 向右平移,设平移距离为
向右平移,设平移距离为![]() .思考:点E落在边
.思考:点E落在边![]() 上时,求半圆
上时,求半圆![]() 与矩形
与矩形![]() 重合部分的面积
重合部分的面积![]() ;
;
(3)探究:在平移过程中,当半圆![]() 与矩形
与矩形![]() 的边相切时,直接写出
的边相切时,直接写出![]() 的值(参考数据:
的值(参考数据:![]() 结果保留根号)
结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com