
【题目】上海市为了增强居民的节水意识,避免水资源的浪费,全面实施居民“阶梯水价”.当累计水量达到年度阶梯水量分档基数临界点后,即开始实施阶梯价格计价,分档水量和价格见下表.
分档 | 户年用水量 (立方米) | 自来水价格 (元/立方米) | 污水处理费 (元/立方米) |
第一阶梯 | 0-220(含220) | 1.92 | 1.70 |
第二阶梯 | 220-300(含300) | 3.30 | 1.70 |
第三阶梯 | 300以上 | 4.30 | 1.70 |
注:1.应缴纳水费 = 自来水费总额 + 污水处理费总额 2.应缴纳污水处理费总额 = 用水量×污水处理费× 0.9 | |||
仔细阅读上述材料,请解答下面的问题,并把答案写在答题纸上:
(1)小静家2019年上半年共计用水量100立方米,应缴纳水费 元;
(2)小静家全年缴纳的水费共计1000.5元,那么2019年全年用水量为 立方米;
(3)如图所示是上海市“阶梯水价”y与用水量x的函数关系,那么第二阶梯(线段AB)的函数解析式为 ,定义域 .
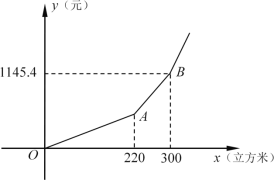
【答案】(1)345; (2)270;(3)![]() ,
,![]() .
.
【解析】
(1)用水量100立方米处于第一阶梯,直接利用应缴纳水费 = 自来水费总额 + 污水处理费总额计算即可;
(2)先判断出用水量处于第几阶梯,然后设2019年全年用水量为x立方米,列出方程求解即可;
(3)先求出用水量220立方米时的水费,然后利用待定系数法求解析式即可,定义域根据图象直接可得.
(1)![]() (元)
(元)
∴用水量100立方米应缴纳水费345元;
(2)当用水量为220立方米时,应缴水费为![]() (元)
(元)
当用水量为300立方米时,应缴水费为![]() (元)
(元)
∴全年缴纳的水费共计1000.5元,说明用水量处于第二阶梯,
设2019年全年用水量为x立方米,根据题意得
![]()
解得![]()
∴2019年全年用水量为270立方米;
(3)由(2)可知,当![]() 时,
时,![]() ,
,
设线段AB的解析式为![]()
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴线段AB的解析式为![]() ,
,
定义域为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校在一次大课间活动中,采用了四种活动形式:A:跑步;B:跳绳;C:做操;D:游戏,全校学生都选择了一种形式参与活动,小明对同学们选择的活动形式进行了随机抽样调查,并绘制了不完整的两幅统计图(如图):
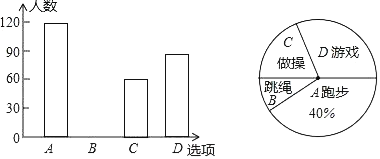
(1)本次共调查了多少名学生?
(2)跳绳B对应扇形的圆心角为多少度?
(3)学校在每班A、B、C、D四种活动形式中,随机抽取两种开展活动,求每班抽取的两种形式恰好是“做操”和“跳绳”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
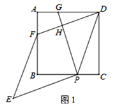
【题目】将大小两把含30°角的直角三角尺按如图1 位置摆放,即大小直角三角尺的直角顶点C 重合,小三角尺的顶点 D、E 分别在大三角尺的直角边 AC、BC 上,此时小三角尺的斜边 DE 恰好经过大三角尺的重心G .已知A CDE 30°, AB 12 .
(1)求小三角尺的直角边CD 的长;
(2)将小三角尺绕点C 逆时针旋转,当点D第一次落在大三角尺的边 AB 上时(如图2),求点 B 、 E 之间的距离;
(3)在小三角尺绕点C 旋转的过程中,当直线 DE 经过点 A 时,求BAE 的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,点P在直线BC上,点G在直线AD上(P,G不与正方形顶点重合,且在CD的同侧),PD=PG,DF⊥PG于点H,交直线AB于点F,将线段PG绕点P逆时针旋转90°得到线段PE,连结EF.
(1)如图1,当点P与点G分别在线段BC与线段AD上时.
①求证:DF=PG;
②若AB=3,PC=1,求四边形PEFD 的面积;
(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD 是怎样的特殊四边形,并证明你的猜想.
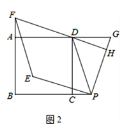
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+b与双曲线![]() 交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线
交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线![]() 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线![]() 于点N.
于点N.
(1)当点A的横坐标为1时,求b的值:
(2)在(1)的条件下,设P点的横坐标为m,
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )

A.![]() n mileB.60 n mileC.120 n mileD.
n mileB.60 n mileC.120 n mileD.![]() n mile
n mile
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
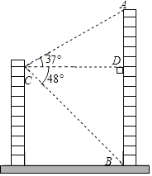
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
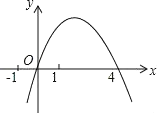
A.t>﹣5B.﹣5<t<3C.3<t≤4D.﹣5<t≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且与反比例函数
,且与反比例函数![]() 在第一象限内的图象交于点
在第一象限内的图象交于点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)设点![]() 是
是![]() 轴上的点,若
轴上的点,若![]() 的面积等于6,直接写出点
的面积等于6,直接写出点![]() 的坐标;
的坐标;
(3)设![]() 点是
点是![]() 轴上的点,且
轴上的点,且![]() 为等腰三角形,求
为等腰三角形,求![]() 点的坐标.
点的坐标.
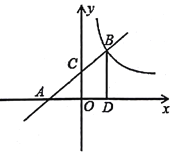
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com