
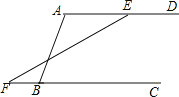
【题目】如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°
,tan72°![]() )
)
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
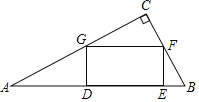
【题目】如图,在△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上,设AG=5,AD=4,求△ADG与△FEB的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+b与双曲线![]() 交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线
交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线![]() 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线![]() 于点N.
于点N.
(1)当点A的横坐标为1时,求b的值:
(2)在(1)的条件下,设P点的横坐标为m,
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
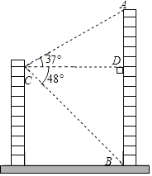
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
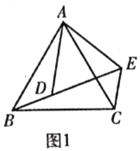
【题目】(1)(问题发现)如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上.填空:①线段
在同一条直线上.填空:①线段![]() ,
,![]() 之间的数量关系为______;②
之间的数量关系为______;②![]() _____°.
_____°.
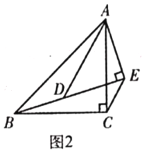
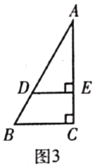
(2)(类比探究)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,请判断线段
在同一条直线上,请判断线段![]() ,
,![]() 之间的数量关系及
之间的数量关系及![]() 的度数,并给出证明.
的度数,并给出证明.
(3)(解决问题)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() 于点
于点![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 所在直线经过点
所在直线经过点![]() 时,
时,![]() 的长是多少?(直接写出答案)
的长是多少?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )
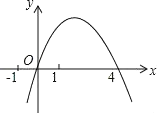
A.t>﹣5B.﹣5<t<3C.3<t≤4D.﹣5<t≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E分别在边AB、AC上,则在下列五个条件中:①∠AED=∠B;②DE∥BC;③![]() =
=![]() ;④AD·BC=DE·AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
;④AD·BC=DE·AC;⑤∠ADE=∠C,能满足△ADE∽△ACB的条件有( )
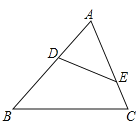
A.1个B.2C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)当每件衬衫降价多少元时,商场每天获利最大,每天获利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
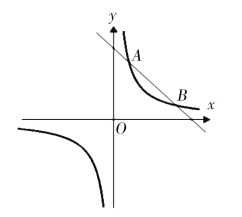
【题目】如图,双曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,点P是x轴上一动点.
,点P是x轴上一动点.
(1)求双曲线![]() 与直线
与直线![]() 的解析式;
的解析式;
(2)当![]() 时,直接写出x的取值范围;
时,直接写出x的取值范围;
(3)当![]() 是等腰三角形时,求点P的坐标.
是等腰三角形时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com