
،¾جâؤ؟،؟ب¥ؤê5شآ·ف£¬خزتذؤ³ضذر§؟ھص¹صù×ِ،°خه؛أذ،¹«أٌ،±ص÷خؤ±ببü»î¶¯£¬بü؛َثو»ْ³éب،ءث²؟·ض²خبüر§ةْµؤ³ة¼¨£¬°´µأ·ض»®·ضخھ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ثؤ¸ِµب¼¶£¬²¢»وضئءثبçدآ²»حêصûµؤئµت·ض²¼±ي؛حةبذخح³¼ئح¼£؛
ثؤ¸ِµب¼¶£¬²¢»وضئءثبçدآ²»حêصûµؤئµت·ض²¼±ي؛حةبذخح³¼ئح¼£؛
µب¼¶ | ³ة¼¨£¨ | ئµت£¨بثت£© |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
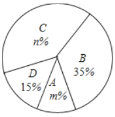
¸ù¾فزشةدذإد¢£¬½â´ًزشدآختجâ£؛
£¨1£©±يضذµؤ![]() £»
£»
£¨2£©ةبذخح³¼ئح¼ضذ![]() £¬
£¬![]() £¬
£¬![]() µب¼¶¶شس¦µؤةبذخµؤش²ذؤ½اخھ ¶ب£»
µب¼¶¶شس¦µؤةبذخµؤش²ذؤ½اخھ ¶ب£»
£¨3£©¸أذ£×¼±¸´سةدتِ»ٌµأ![]() µب¼¶6أûر§ةْضذر،ب،ء½بث×ِخھر§ذ£،°خه؛أذ،¹«أٌ،±ض¾ش¸صك£¬زرضھصâ6بثضذسذ3أûؤذةْ£¨سأ
µب¼¶6أûر§ةْضذر،ب،ء½بث×ِخھر§ذ£،°خه؛أذ،¹«أٌ،±ض¾ش¸صك£¬زرضھصâ6بثضذسذ3أûؤذةْ£¨سأ![]() £¬
£¬![]() £¬
£¬![]() ±يت¾£©؛ح3أûإ®ةْ£¨سأ
±يت¾£©؛ح3أûإ®ةْ£¨سأ![]() £¬
£¬![]() £¬
£¬![]() ±يت¾£©£¬اëسأءذ±ي»ٍ»ت÷×´ح¼µؤ·½·¨اَا،؛أر،ب،µؤتا
±يت¾£©£¬اëسأءذ±ي»ٍ»ت÷×´ح¼µؤ·½·¨اَا،؛أر،ب،µؤتا![]() ؛ح
؛ح![]() µؤ¸إآت£®
µؤ¸إآت£®
،¾´ً°¸،؟£¨1£©21£»£¨2£©10،¢40،¢144£»£¨3£©ا،؛أر،ب،µؤتا![]() ؛ح
؛ح![]() µؤ¸إآتخھ
µؤ¸إآتخھ![]() £®
£®
،¾½âخِ،؟
£¨1£©ہûسأDµب¼¶µؤبثت³زشئنثùص¼µ÷²é×ـبثتµؤ°ظ·ضآت¼´؟ةاَ³ِµ÷²é×ـبثت£¬ب»؛َہûسأµ÷²é×ـبثت¼ُب¥Aµب¼¶،¢Cµب¼¶،¢Dµب¼¶µؤبثت¼´؟ةاَ³ِx£»
£¨2£©ہûسأAµب¼¶بثت³زشµ÷²é×ـبثت¼´؟ةاَ³ِmµؤضµ£¬ہûسأCµب¼¶بثت³زشµ÷²é×ـبثت¼´؟ةاَ³ِnµؤضµ£¬´س¶ّاَ³ِ![]() µب¼¶¶شس¦µؤةبذخµؤش²ذؤ½ا£»
µب¼¶¶شس¦µؤةبذخµؤش²ذؤ½ا£»
£¨3£©¸ù¾فجâز⣬ءذ³ِ±ي¸ٌ£¬ب»؛َ¸ù¾ف¸إآت¹«ت½¼ئثم¼´؟ة£®
½â£؛£¨1£©µ÷²é×ـبثتخھ9،آ15%=60£¨بث£©
،àx=60£6£24£9=21
¹ت´ً°¸خھ£؛21£»
£¨2£©m%=6،آ60=10%£¬n%=24،آ60=40%
،àm=10£¬n=40
![]() µب¼¶¶شس¦µؤةبذخµؤش²ذؤ½اخھ40%،ء360،م=144،م
µب¼¶¶شس¦µؤةبذخµؤش²ذؤ½اخھ40%،ء360،م=144،م
¹ت´ً°¸خھ£؛10£»40£»144£»
£¨3£©ءذ±يبçدآ£؛

¹²سذ30ضضµب؟ةؤـµؤ½ل¹û£¬ئنضذا،؛أر،ب،µؤتا![]() ؛ح
؛ح![]() µؤ½ل¹ûسذ2ضض
µؤ½ل¹ûسذ2ضض
¹تا،؛أر،ب،µؤتا![]() ؛ح
؛ح![]() µؤ¸إآتخھ2،آ30=
µؤ¸إآتخھ2،آ30=![]() £®
£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شؤ¶ءدآءذ²ؤءد£¬²¢حê³ةدàس¦µؤبخخٌ£®
حذہصأـ¶¨ہي£؛
حذہصأـ£¨Ptolemy£©£¨¹«شھ90ؤê،«¹«شھ168ؤ꣩£¬د£ہ°ضّأûµؤجىخؤر§¼ز£¬ثûµؤزھضّ×÷،¶جىخؤر§´َ³ة،·±»؛َبث³ئخھ،°خ°´َµؤتر§تé،±£¬حذہصأـسذت±°رثü½ذ×÷،¶تر§خؤ¼¯،·£¬حذہصأـ´ستéضذصھ³ِ²¢¼سزشحêةئ£¬µأµ½ءثضّأûµؤحذہصأـ£¨Ptolemy£©¶¨ہي£®

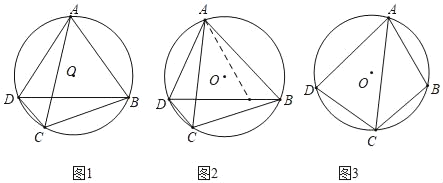
حذہصأـ¶¨ہي£؛
ش²ؤع½سثؤ±كذخضذ£¬ء½جُ¶ش½ادكµؤ³ث»µبسعء½×é¶ش±ك³ث»ض®؛ح£®
زرضھ£؛بçح¼1£¬ثؤ±كذخABCDؤع½سسع،رO£¬
اَض¤£؛ABCD+BCAD£½ACBD
دآأوتا¸أ½لآغµؤض¤أ÷¹³ج£؛
ض¤أ÷£؛بçح¼2£¬×÷،دBAE£½،دCAD£¬½»BDسعµمE£®
،ك![]()
،à،دABE£½،دACD
،à،÷ABE،×،÷ACD
،à![]()
،àABCD£½ACBE
،ك![]()
،à،دACB£½،دADE£¨زہ¾ف1£©
،ك،دBAE£½،دCAD
،à،دBAE+،دEAC£½،دCAD+،دEAC
¼´،دBAC£½،دEAD
،à،÷ABC،×،÷AED£¨زہ¾ف2£©
،àADBC£½ACED
،àABCD+ADBC£½AC£¨BE+ED£©
،àABCD+ADBC£½ACBD
بخخٌ£؛£¨1£©ةدتِض¤أ÷¹³جضذµؤ،°زہ¾ف1،±،¢،°زہ¾ف2،±·ض±ًتاض¸ت²أ´£؟
£¨2£©µ±ش²ؤع½سثؤ±كذخABCDتا¾طذخت±£¬حذہصأـ¶¨ہي¾حتاخزأا·ا³£تىضھµؤز»¸ِ¶¨ہي£؛،، ،،£®
£¨اëذ´³ِ£©
£¨3£©بçح¼3£¬ثؤ±كذخABCDؤع½سسع،رO£¬AB£½3£¬AD£½5£¬،دBAD£½60،م£¬µمCخھ![]() µؤضذµم£¬اَACµؤ³¤£®
µؤضذµم£¬اَACµؤ³¤£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
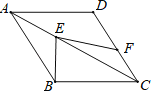
،¾جâؤ؟،؟بçح¼£¬شعءâذخABCDضذ£¬µمEشع¶ش½ادكACةد£¬µمFشع±كCDةد£¬ء¬½سBE،¢EF£®بô،دEFC£½90،م+![]() ،دCBE£¬BE£½7£¬EF£½10£®شٍµمDµ½EFµؤ¾àہëخھ_____£®
،دCBE£¬BE£½7£¬EF£½10£®شٍµمDµ½EFµؤ¾àہëخھ_____£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
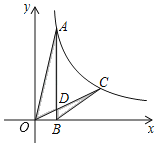
،¾جâؤ؟،؟بçح¼£¬زرضھµمA£¬µمCشع·´±بہ؛¯تy£½![]() £¨k£¾0£¬x£¾0£©µؤح¼دَةد£¬AB،حxضلسعµمB£¬OC½»ABسعµمD£¬بôCD£½OD£¬شٍ،÷AODسë،÷BCDµؤأو»±بخھ__£®
£¨k£¾0£¬x£¾0£©µؤح¼دَةد£¬AB،حxضلسعµمB£¬OC½»ABسعµمD£¬بôCD£½OD£¬شٍ،÷AODسë،÷BCDµؤأو»±بخھ__£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬إ×خïدك![]() µؤ¶ش³ئضلخھض±دك
µؤ¶ش³ئضلخھض±دك![]() £¬سë
£¬سë![]() ضلµؤز»¸ِ½»µمشع
ضلµؤز»¸ِ½»µمشع![]() ؛ح
؛ح![]() ض®¼ن£¬ئن²؟·ضح¼دَبçح¼ثùت¾£®شٍدآءذ½لآغ£؛¢ظ
ض®¼ن£¬ئن²؟·ضح¼دَبçح¼ثùت¾£®شٍدآءذ½لآغ£؛¢ظ![]() £»¢ع
£»¢ع![]() £»¢غ
£»¢غ![]() £»¢ـ
£»¢ـ![]() £¨
£¨![]() خھتµت£©£»¢فµم
خھتµت£©£»¢فµم![]() £¬
£¬![]() £¬
£¬![]() تا¸أإ×خïدكةدµؤµم£¬شٍ
تا¸أإ×خïدكةدµؤµم£¬شٍ![]() £¬ئنضذ£¬صب·½لآغµؤ¸ِتتا£¨ £©
£¬ئنضذ£¬صب·½لآغµؤ¸ِتتا£¨ £©
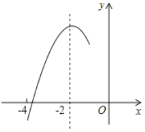
A.1B.2C.3D.4
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ذ£خھءث½â¸أذ£³ُبر§ةْ¾س¼زر§د°ئع¼ن²خ¼س،°حّآç×شد°تز،±×شض÷ر§د°µؤاé؟ِ£¬ثو»ْ³é²éءث²؟·ضر§ةْشعء½ضـؤع²خ¼س،°حّآç×شد°تز،±×شض÷ر§د°µؤجىت£¬²¢سأµأµ½µؤت¾ف»وضئءثبçدآء½·ù²»حêصûµؤح³¼ئح¼£®
اë¸ù¾فح¼ضذجل¹©µؤذإد¢£¬»ط´ًدآءذختج⣮
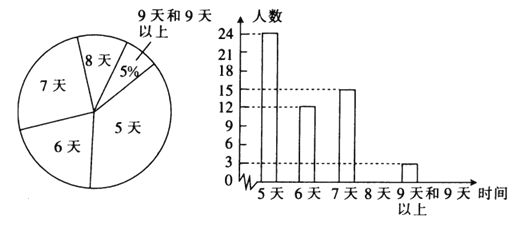
£¨1£©²¹ب«جُذخح³¼ئح¼£®
£¨2£©²؟·ضر§ةْشعء½ضـؤع²خ¼س،°حّآç×شد°تز،±×شض÷ر§د°جىتµؤضعتخھ______£¬ضذخ»تخھ________£»
£¨3£©بç¹û¸أذ£³ُبؤ꼶ش¼سذ![]() أûر§ةْ£¬اëؤم¹ہ¼ئشعصâء½ضـؤعب«ذ£³ُبؤ꼶؟ةؤـسذ¶àةظأûر§ةْ²خ¼س،°حّآç×شد°تز،±×شض÷ر§د°µؤجىت²»ةظسع
أûر§ةْ£¬اëؤم¹ہ¼ئشعصâء½ضـؤعب«ذ£³ُبؤ꼶؟ةؤـسذ¶àةظأûر§ةْ²خ¼س،°حّآç×شد°تز،±×شض÷ر§د°µؤجىت²»ةظسع![]() جى£®
جى£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬زرضھإ×خïدكy£½ax2+![]() x+c¾¹A£¨4£¬0£©£¬B£¨1£¬0£©ء½µم£¬سëyضل½»سعµمC£®
x+c¾¹A£¨4£¬0£©£¬B£¨1£¬0£©ء½µم£¬سëyضل½»سعµمC£®
£¨1£©اَ¸أإ×خïدكµؤ½âخِت½£»
£¨2£©شعض±دكACةد·½µؤإ×خïدكةدتا·ٌ´وشعز»µمD£¬ت¹µأ،÷DCAµؤأو»×î´َ£؟بô´وشع£¬اَ³ِµمDµؤ×ّ±ê¼°،÷DCAأو»µؤ×î´َضµ£»بô²»´وشع£¬اëثµأ÷ہيسة£®
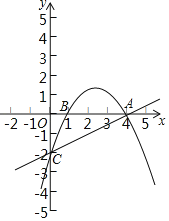
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شؤ¶ءدآأوµؤ²ؤءد£؛
بç¹û؛¯ت y£½f£¨x£©آْ×م£؛¶شسع×ش±نء؟ x µؤب،ضµ·¶خ§ؤعµؤبخزâ x1£¬x2£¬
£¨1£©بô x1£¼x2£¬¶¼سذ f£¨x1£©£¼f£¨x2£©£¬شٍ³ئ f£¨x£©تاشِ؛¯ت£»
£¨2£©بô x1£¼x2£¬¶¼سذ f£¨x1£©£¾f£¨x2£©£¬شٍ³ئ f£¨x£©تا¼ُ؛¯ت£®
ہجâ£؛ض¤أ÷؛¯تf£¨x£©£½![]() £¨x£¾0£©تا¼ُ؛¯ت£®
£¨x£¾0£©تا¼ُ؛¯ت£®
ض¤أ÷£؛ةè 0£¼x1£¼x2£¬
f£¨x1£©©پf£¨x2£©£½![]() £®
£®
،ك0£¼x1£¼x2£¬
،àx2©پx1£¾0£¬x1x2£¾0£®
،à![]() £¾0£®¼´ f£¨x1£©©پf£¨x2£©£¾0£®
£¾0£®¼´ f£¨x1£©©پf£¨x2£©£¾0£®
،àf£¨x1£©£¾f£¨x2£©£®
،à؛¯ت f£¨x£©=![]() £¨x£¾0£©تا¼ُ؛¯ت£®
£¨x£¾0£©تا¼ُ؛¯ت£®
¸ù¾فزشةد²ؤءد£¬½â´ًدآأوµؤختجâ£؛
زرضھ؛¯ت![]() £®
£®
f£¨©پ1£©£½![]() +£¨©پ2£©£½-1£¬f£¨©پ2£©£½
+£¨©پ2£©£½-1£¬f£¨©پ2£©£½![]() +£¨©پ4£©£½
+£¨©پ4£©£½![]() £®
£®
£¨1£©¼ئثم£؛f£¨©پ3£©£½ £¬f£¨©پ4£©£½ £»
£¨2£©²آدë£؛؛¯ت![]() تا ؛¯ت£¨جî،°شِ،±»ٍ،°¼ُ،±£©£»
تا ؛¯ت£¨جî،°شِ،±»ٍ،°¼ُ،±£©£»
£¨3£©اë·آصصہجâض¤أ÷ؤمµؤ²آد룮
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ض±¾¶خھ10µؤ،رA¾¹µمC(0,5)؛حµمO (0,0)£¬Bتاyضلسز²à،رAسإ»،ةدز»µم,شٍ،دOBC µؤسàدزضµخھ _________________.
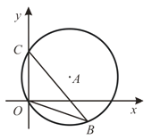
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com