
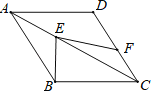
【题目】如图,在菱形ABCD中,点E在对角线AC上,点F在边CD上,连接BE、EF.若∠EFC=90°+![]() ∠CBE,BE=7,EF=10.则点D到EF的距离为_____.
∠CBE,BE=7,EF=10.则点D到EF的距离为_____.
【答案】2![]()
【解析】
连接DE,过D作DG⊥EF于G,由菱形的性质得到AB=AD,∠BAE=∠DAE,从而证得△ABE≌△ADE,进而求得∠CBE=∠CDE,然后结合题目条件和等量代换求得∠EDG=![]() ∠CDE=∠FDG,进而用ASA定理证明△EDG≌△FDG,得到ED=DF,BE=DF=7,GE=
∠CDE=∠FDG,进而用ASA定理证明△EDG≌△FDG,得到ED=DF,BE=DF=7,GE=![]() EF=5,然后利用勾股定理求解即可得到结论.
EF=5,然后利用勾股定理求解即可得到结论.
解:连接DE,过D作DG⊥EF于G,则∠DEF+∠EDG=90°,
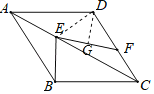
∵四边形ABCD是菱形,
∴AB=AD,∠BAE=∠DAE,
∵AE=AE,
∴△ABE≌△ADE(SAS),
∴BE=DE,∠ABE=∠ADE,
∵∠ABC=∠ADC,
∴∠CBE=∠CDE,
∵∠EFC=∠CDE+∠DEF,∠EFC=90°+![]() ∠CBE,
∠CBE,
∴90°+![]() ∠CBE=∠CDE+∠DEF,
∠CBE=∠CDE+∠DEF,
∴![]() ∠CDE+∠DEF=90°,
∠CDE+∠DEF=90°,
∴∠EDG=![]() ∠CDE=∠FDG,
∠CDE=∠FDG,
∵DG=DG,∠DGE=∠DGF=90°,
∴△EDG≌△FDG(ASA),
∴ED=DF,
∴BE=DF=7,
∴GE=![]() EF=5,
EF=5,
∴在Rt△DGE中,DG=![]() ,
,
∴点D到EF的距离为2![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
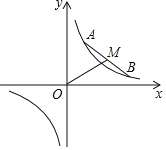
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上运动,且始终保持线段
的图象上运动,且始终保持线段![]() 的长度不变.
的长度不变.![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() .则线段
.则线段![]() 长度的最小值是_____(用含
长度的最小值是_____(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
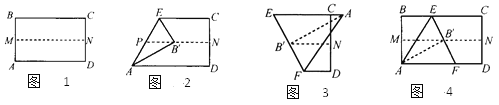
【题目】取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图3.
利用展开图4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横、纵坐标均为整数的点称为格点,如图,![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() 上的点
上的点![]() 也为格点,用无刻度的直尺作图:
也为格点,用无刻度的直尺作图:
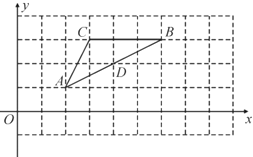
(1)将线段![]() 绕点
绕点![]() 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段![]() ,写出格点
,写出格点![]() 的坐标;
的坐标;
(2)将线段![]() 平移至线段
平移至线段![]() ,使点
,使点![]() 与点
与点![]() 重合,直接写出格点
重合,直接写出格点![]() 的坐标;
的坐标;
(3)画出线段![]() 关于
关于![]() 对称的线段
对称的线段![]() ,保留作图痕迹.
,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
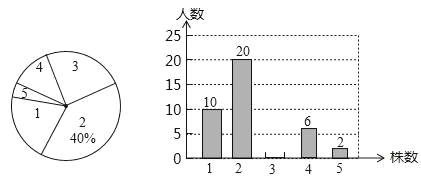
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
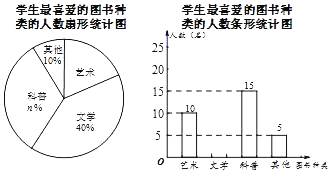
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ,并请根据以上信息补全条形统计图;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)根据抽样调查的结果,请你估计该校900名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩( | 频数(人数) |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
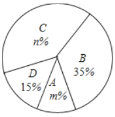
根据以上信息,解答以下问题:
(1)表中的![]() ;
;
(2)扇形统计图中![]() ,
,![]() ,
,![]() 等级对应的扇形的圆心角为 度;
等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得![]() 等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用
等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用![]() ,
,![]() ,
,![]() 表示)和3名女生(用
表示)和3名女生(用![]() ,
,![]() ,
,![]() 表示),请用列表或画树状图的方法求恰好选取的是
表示),请用列表或画树状图的方法求恰好选取的是![]() 和
和![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
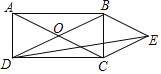
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,AB:BC=2:1,且BE∥AC,CE∥DB,连接DE,则tan∠EDC=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com