练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在ABCD中，E、F为边BC上两点，BF＝CE，AE＝DF．

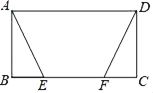
    （1）求证：△ABE≌△DCF；（2）求证：四边形ABCD是矩形．

    【答案】（1）见解析；（2）见解析.

    【解析】

    （1）根据平行四边形的性质得到AB＝DC．根据全等三角形的判定定理即可得到结论．

    （2）根据全等三角形的性质得到∠B＝∠C．根据平行四边形的性质得到AB∥CD．根据矩形的判定定理即可得到结论．

    （1）证明：∵四边形ABCD是平行四边形，

    ∴AB＝DC．

    ∵BF＝CE，

    ∴BF﹣EF＝CE﹣EF，

    ∴BE＝CF．

    在△ABE和△DCF中，

    ∵，

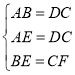    ∴△ABE≌△DCF（SSS）；

    （2）证明：∵△ABE≌△DCF，

    ∴∠B＝∠C．

    ∵四边形ABCD是平行四边形，

    ∴AB∥CD．

    ∴∠B+∠C＝180°．

    ∴∠B＝∠C＝90°．

    ∵四边形ABCD是平行四边形，∠B＝90°，

    ∴四边形ABCD是矩形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某超市要进一批鸡蛋进行销售，有、两家农场可供货．为了比较两家提供的鸡蛋单个大小，超市分别对这两家农场的鸡蛋进行抽样检测，通过分析数据确定鸡蛋的供货商．

    （1）下列抽样方式比较合理的是哪一种？请简述原因．

    ①分别从、两家提供的一箱鸡蛋中拿出最上面的两层（共40枚）鸡蛋，并分别称出其中每一个鸡蛋的质量．

    ②分别从、两家提供的一箱鸡蛋中每一层随机抽4枚（共40枚）鸡蛋，并分别称出其中每个鸡蛋的质量．

    （2）在用合理的方法抽出两家提供的鸡蛋各40枚后，分别称出每个鸡蛋的质量（单位：），结果如表所示（数据包括左端点不包括右端点）．

    45～47

    47～49

    49～51

    51～53

    53～55

    农场鸡蛋

    2

    8

    15

    10

    5

    农场鸡蛋

    4

    6

    12

    14

    4

    ①如果从这两家农场提供的鸡蛋中随机拿一个，分别估计两家鸡蛋质量在（单位：）范围内的概率（数据包括左端点不包括右端点）；

    ②如果你是超市经营者，试通过数据分析确定选择哪家农场提供的鸡蛋．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并完成相应的任务．

    托勒密定理：

    托勒密（Ptolemy）（公元90年～公元168年），希腊著名的天文学家，他的要著作《天文学大成》被后人称为“伟大的数学书”，托勒密有时把它叫作《数学文集》，托勒密从书中摘出并加以完善，得到了著名的托勒密（Ptolemy）定理．

    托勒密定理：

    圆内接四边形中，两条对角线的乘积等于两组对边乘积之和．

    已知：如图1，四边形ABCD内接于⊙O，

    求证：ABCD+BCAD＝ACBD

    下面是该结论的证明过程：

    证明：如图2，作∠BAE＝∠CAD，交BD于点E．

    ∵

    ∴∠ABE＝∠ACD

    ∴△ABE∽△ACD

    ∴

    ∴ABCD＝ACBE

    ∵

    ∴∠ACB＝∠ADE（依据1）

    ∵∠BAE＝∠CAD

    ∴∠BAE+∠EAC＝∠CAD+∠EAC

    即∠BAC＝∠EAD

    ∴△ABC∽△AED（依据2）

    ∴ADBC＝ACED

    ∴ABCD+ADBC＝AC（BE+ED）

    ∴ABCD+ADBC＝ACBD

    任务：（1）上述证明过程中的“依据1”、“依据2”分别是指什么？

    （2）当圆内接四边形ABCD是矩形时，托勒密定理就是我们非常熟知的一个定理：　 　．

    （请写出）

    （3）如图3，四边形ABCD内接于⊙O，AB＝3，AD＝5，∠BAD＝60°，点C为的中点，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形中，连接点为上一点，使得连接交于点，作交的延长线于点．

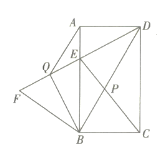
    （1）求证：．

    （2）若求的长．

    （3）在（2）的条件下，将沿着对折得到点的对应点为点，连接试求的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，反比例函数y= 的图象与一次函数y=x+b的图象交

    于点A（1，4）、点B（-4，n）．

    （1）求一次函数和反比例函数的解析式；

    （2）求△OAB的面积；

    （3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一张半径为的圆形纸片，点为圆心，将该圆形纸片沿直线折叠，直线交于两点．

    （1）若折叠后的圆弧恰好经过点，利用直尺和圆规在图中作出满足条件的一条直线（不写作法，保留作图痕迹），并求此时线段的长度．

    （2）已知是一点，．

    ①若折叠后的圆弧经过点，则线段长度的取值范围是________．

    ②若折叠后的圆弧与直线相切于点，则线段的长度为_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

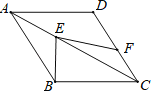
    【题目】如图，在菱形ABCD中，点E在对角线AC上，点F在边CD上，连接BE、EF．若∠EFC＝90°+∠CBE，BE＝7，EF＝10．则点D到EF的距离为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

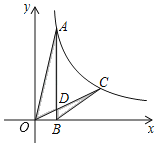
    【题目】如图，已知点A，点C在反比例函数y＝（k＞0，x＞0）的图象上，AB⊥x轴于点B，OC交AB于点D，若CD＝OD，则△AOD与△BCD的面积比为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的材料：

    如果函数 y＝f（x）满足：对于自变量 x 的取值范围内的任意 x1，x2，

    （1）若 x1＜x2，都有 f（x1）＜f（x2），则称 f（x）是增函数；

    （2）若 x1＜x2，都有 f（x1）＞f（x2），则称 f（x）是减函数．

    例题：证明函数f（x）＝ （x＞0）是减函数．

    证明：设 0＜x1＜x2，

    f（x1）﹣f（x2）＝．

    ∵0＜x1＜x2，

    ∴x2﹣x1＞0，x1x2＞0．

    ∴＞0．即 f（x1）﹣f（x2）＞0．

    ∴f（x1）＞f（x2）．

    ∴函数 f（x）= （x＞0）是减函数．

    根据以上材料，解答下面的问题：

    已知函数．

    f（﹣1）＝ +（﹣2）＝-1，f（﹣2）＝ +（﹣4）＝．

    （1）计算：f（﹣3）＝ ，f（﹣4）＝ ；

    （2）猜想：函数是 函数（填“增”或“减”）；

    （3）请仿照例题证明你的猜想．

    查看答案和解析>>

    同步练习册答案