
【题目】阅读下列材料,并完成相应的任务.
托勒密定理:
托勒密(Ptolemy)(公元90年~公元168年),希腊著名的天文学家,他的要著作《天文学大成》被后人称为“伟大的数学书”,托勒密有时把它叫作《数学文集》,托勒密从书中摘出并加以完善,得到了著名的托勒密(Ptolemy)定理.

托勒密定理:
圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.
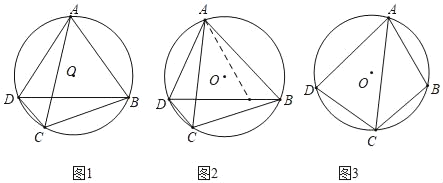
已知:如图1,四边形ABCD内接于⊙O,
求证:ABCD+BCAD=ACBD
下面是该结论的证明过程:
证明:如图2,作∠BAE=∠CAD,交BD于点E.
∵![]()
∴∠ABE=∠ACD
∴△ABE∽△ACD
∴![]()
∴ABCD=ACBE
∵![]()
∴∠ACB=∠ADE(依据1)
∵∠BAE=∠CAD
∴∠BAE+∠EAC=∠CAD+∠EAC
即∠BAC=∠EAD
∴△ABC∽△AED(依据2)
∴ADBC=ACED
∴ABCD+ADBC=AC(BE+ED)
∴ABCD+ADBC=ACBD
任务:(1)上述证明过程中的“依据1”、“依据2”分别是指什么?
(2)当圆内接四边形ABCD是矩形时,托勒密定理就是我们非常熟知的一个定理: .
(请写出)
(3)如图3,四边形ABCD内接于⊙O,AB=3,AD=5,∠BAD=60°,点C为![]() 的中点,求AC的长.
的中点,求AC的长.
【答案】(1)上述证明过程中的“依据1”是同弧所对的圆周角相等.“依据2”是两角分别相等的两个三角形相似;(2) 勾股定理;(3) ![]() .
.
【解析】
(1)根据圆周角定理,相似三角形的判定即可解决问题.
(2)利用矩形的性质以及托勒密定理即可判断.
(3)连接BD,作CE⊥BD于E.首先证明BD=2DE=![]() CD,由托勒密定理,构建方程求出AC即可.
CD,由托勒密定理,构建方程求出AC即可.
(1)上述证明过程中的“依据1”是同弧所对的圆周角相等.
“依据2”是两角分别相等的两个三角形相似.
(2)当圆内接四边形ABCD是矩形时,
则AB=CD,AD=BC,AC=BD,
∵ABCD+ADBC=ACBD,
∴AB2+AD2=BD2,
托勒密定理就是我们非常熟知的一个定理:勾股定理,
故答案为勾股定理.
(3)连接BD,作CE⊥BD于E.

∵四边形ABCD是圆内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BAD=60°,
∴∠BCD=120°,
∵![]() ,
,
∴CD=CB,
∴∠CDB=30°,
在Rt△CDE中,cos30°=![]() ,
,
∴DE=![]() CD,
CD,
∴BD=2DE=![]() CD,
CD,
由托勒密定理:ACBD=ADBC+CDAB,
∴AC![]() CD=3CD+5CD,
CD=3CD+5CD,
∴AC=![]() ,
,
答:AC的长为![]() .
.


科目:初中数学 来源: 题型:
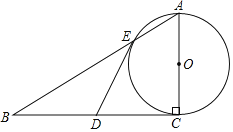
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
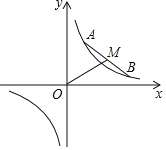
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上运动,且始终保持线段
的图象上运动,且始终保持线段![]() 的长度不变.
的长度不变.![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() .则线段
.则线段![]() 长度的最小值是_____(用含
长度的最小值是_____(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、F分别是BC、AC边的中点,连接DA、DF,且AD=2DF,过点B作AD的平行线交FD的延长线于点E.
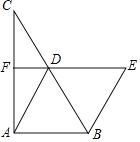
(1)求证:四边形ABED为菱形;
(2)若BD=6,∠E=60°,求四边形ABEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A、B,使得点P在射线BC上,且∠APB![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时,
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D、E、F中,⊙O的依附点是 ;
②点T在直线y=﹣x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为2,直线y=﹣x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,直接写出圆心C的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,李林和王聪两人在玩转盘游戏时,分别把转盘![]() ,
,![]() 分成3等份和4等份,并标上数字(如图所示).游戏规则:同时转动两个转盘,当两转盘停止后,若指针所指两个数字之和小于4,则李林获胜;若数字之和大于4,则王聪获胜,如果指针落在分割线上,则需要重新转动转盘.
分成3等份和4等份,并标上数字(如图所示).游戏规则:同时转动两个转盘,当两转盘停止后,若指针所指两个数字之和小于4,则李林获胜;若数字之和大于4,则王聪获胜,如果指针落在分割线上,则需要重新转动转盘.
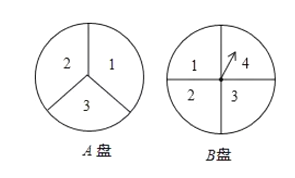
(1)用列表法或画树状图法中的一种方法,求所有可能出现的结果.
(2)该游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
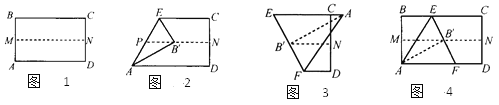
【题目】取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图3.
利用展开图4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩( | 频数(人数) |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
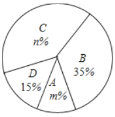
根据以上信息,解答以下问题:
(1)表中的![]() ;
;
(2)扇形统计图中![]() ,
,![]() ,
,![]() 等级对应的扇形的圆心角为 度;
等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得![]() 等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用
等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用![]() ,
,![]() ,
,![]() 表示)和3名女生(用
表示)和3名女生(用![]() ,
,![]() ,
,![]() 表示),请用列表或画树状图的方法求恰好选取的是
表示),请用列表或画树状图的方法求恰好选取的是![]() 和
和![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com