
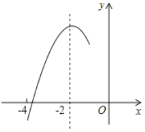
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示.则下列结论:①
之间,其部分图象如图所示.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (
(![]() 为实数);⑤点
为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ,其中,正确结论的个数是( )
,其中,正确结论的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
根据对称轴公式可得![]() ,即可判断①;然后根据抛物线的对称轴和与x轴的交点坐标即可判断抛物线与
,即可判断①;然后根据抛物线的对称轴和与x轴的交点坐标即可判断抛物线与![]() 轴的另一个交点在
轴的另一个交点在![]() 和
和![]() 之间,从而判断②和③;由图象可得当x=-2时,y取最大值,最大值为
之间,从而判断②和③;由图象可得当x=-2时,y取最大值,最大值为![]() ,从而判断④;最后利用抛物线的对称性和增减性即可判断⑤.
,从而判断④;最后利用抛物线的对称性和增减性即可判断⑤.
解:∵抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,
∴![]()
解得:b=4a
∴![]() ,故①正确;
,故①正确;
∵抛物线与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,
之间,
∴抛物线与![]() 轴的另一个交点在
轴的另一个交点在![]() 和
和![]() 之间,
之间,
∴当x=0时,y<0;当x=-1时,y>0
∴当x=0时,y=c<0,故②正确;
当x=-1时,y=a-b+c>0
∴a-4a+c>0
解得:![]() ,故③错误;
,故③错误;
由图象可得当x=-2时,y取最大值,最大值为![]()
∴当x=t时,![]() ≤
≤![]()
∴![]() ,故④错误;
,故④错误;
![]() 关于直线x=-2的对称点为
关于直线x=-2的对称点为![]()
由抛物线可得当x<-2时,y随x的增大而增大
∵![]()
∴![]() ,故⑤正确
,故⑤正确
综上:正确的结论有3个
故选C.


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A、B,使得点P在射线BC上,且∠APB![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时,
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D、E、F中,⊙O的依附点是 ;
②点T在直线y=﹣x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
(2)⊙C的圆心在x轴上,半径为2,直线y=﹣x+2与x轴、y轴分别交于点M、N,若线段MN上的所有点都是⊙C的依附点,直接写出圆心C的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横、纵坐标均为整数的点称为格点,如图,![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 均为格点,
均为格点,![]() 上的点
上的点![]() 也为格点,用无刻度的直尺作图:
也为格点,用无刻度的直尺作图:
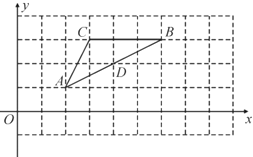
(1)将线段![]() 绕点
绕点![]() 顺时针旋转90°,得到线段
顺时针旋转90°,得到线段![]() ,写出格点
,写出格点![]() 的坐标;
的坐标;
(2)将线段![]() 平移至线段
平移至线段![]() ,使点
,使点![]() 与点
与点![]() 重合,直接写出格点
重合,直接写出格点![]() 的坐标;
的坐标;
(3)画出线段![]() 关于
关于![]() 对称的线段
对称的线段![]() ,保留作图痕迹.
,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
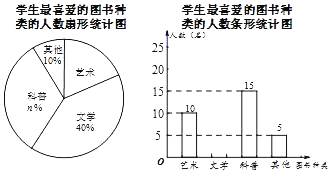
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ,并请根据以上信息补全条形统计图;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)根据抽样调查的结果,请你估计该校900名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩( | 频数(人数) |
|
| 6 |
|
|
|
|
| 24 |
|
| 9 |
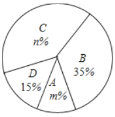
根据以上信息,解答以下问题:
(1)表中的![]() ;
;
(2)扇形统计图中![]() ,
,![]() ,
,![]() 等级对应的扇形的圆心角为 度;
等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得![]() 等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用
等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用![]() ,
,![]() ,
,![]() 表示)和3名女生(用
表示)和3名女生(用![]() ,
,![]() ,
,![]() 表示),请用列表或画树状图的方法求恰好选取的是
表示),请用列表或画树状图的方法求恰好选取的是![]() 和
和![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陕西省相关文件规定,西安市实行居民阶梯水价制度,对居民用水的基本水价实行![]() 三级价差,各阶梯水价均为用户终端水价,具体如下:
三级价差,各阶梯水价均为用户终端水价,具体如下:
第一阶梯:年用水量![]() 及以下,终端水价为
及以下,终端水价为![]() 元/
元/![]() .
.
第二阶梯:年用水量![]() (含),终端水价为
(含),终端水价为![]() 元/
元/![]() .
.
第三阶梯:年用水量![]() 以上,终端水价为
以上,终端水价为![]() 元/
元/![]() .
.
城区居民阶梯水价计量结算周期以年为单位,年用水量累计达到各阶梯水量上限后,超出部分执行下一阶梯水价;年度周期之间水量不结转,不累计.
设某户居民2019年的年用水量为![]() ,应缴水费为
,应缴水费为![]() (元).
(元).
(1)写出该户居民2019年的年用水量为![]() 含)的
含)的![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)若该户居民2019年的应缴水费为![]() 元,则该户居民2019年的年用水量为多少.
元,则该户居民2019年的年用水量为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年五月,我国南方某省A、B两市遭受严重洪涝灾害,邻近县市C、D决定调运物资支援A、B两市灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)A、B两市各需救灾物资多少吨?
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com