
【题目】从下面两题中只选做一题,如果做了两题的,只按第(1)题评分:
(1)用“=>”与“<=”表示一种运算法则:(a=>b)=﹣b,(a<=b)=﹣a,如(2=>3)=﹣3,则(2010=>2011)<=(2009=>2008)=________(括号运算优先)
(2)用“>”或“<”号填空:sin40°cos50°﹣![]() ________0.(可用计算器计算)
________0.(可用计算器计算)
【答案】2011 <
【解析】
(1)首先认真分析找出规律,然后再代入数值计算.
(2)根据cosα=sin(90°-α)和三角函数的增减性计算.
解:(1)(2010=>2011)与(2009=>2008)都符合公式:(a=>b)=-b,
∴(2010=>2011)=-2011,
(2009=>2008)=-2008,
∴(2010=>2011)<=(2009=>2008)=(-2011)<=(-2008),
(-2011)<=(-2008)符合公式(a<=b)=-a,
∴(-2011)<=(-2008)=2011.
(2)∵90°>40°>0°,
∴cos50°=sin(90°-50°)=sin40°,
∴原式=(sin40°)2﹣![]() ,
,
又∵(sin40°)2<(sin45°)2=![]() ,
,
∴(sin40°)2<![]() ,
,
即(sin40°)2﹣![]() <0.
<0.


科目:初中数学 来源: 题型:
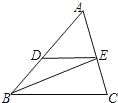
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果![]() =3,
=3,![]() =2,DE=6,求BC的长.
=2,DE=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小琴的父母承包了一块荒山地种植一批梨树,今年收获一批金溪密梨,小琴的父母打算以m元/斤的零售价销售5000斤密梨;剩余的5000(m+1)斤密犁以比零售价低1元的批发价批给外地客商,预计总共可赚得55 000元的毛利润.

(1)求小琴的父母今年共收获金溪密梨多少斤?
(2)若零售金溪密梨平均每天可售出200斤,每斤盈利2元.为了加快销售和获得较好的售价,采取了降价措施,发现销售单价每降低0.1元,平均每天可多售出40斤,应降价多少元?每天销售利润为600元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(-1,0),C(0,-5)两点,与x轴交于点B.
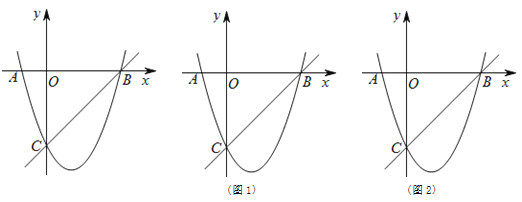
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q. 若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
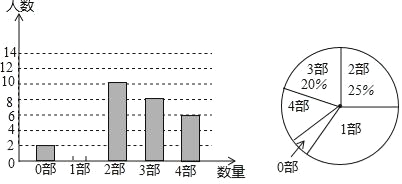
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
(1)本次调查了 名学生,扇形统计图中“1部”所在扇形的圆心角为 度,并补全条形统计图;
(2)此中学共有1600名学生,通过计算预估其中4部都读完了的学生人数;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,求他们选中同一名著的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
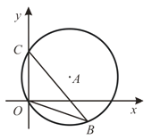
【题目】如图,直径为10的⊙A经过点C(0,5)和点O (0,0),B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为 _________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
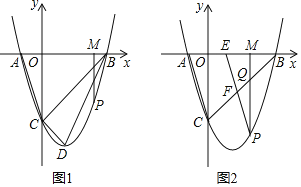
【题目】如图1,抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3),抛物线顶点为D,连接AC,BC,CD,BD,点P是x轴下方抛物线上的一个动点,作PM⊥x轴于点M,设点M的横坐标为m.
(1)求抛物线的解析式及点D的坐标;
(2)试探究是否存在这样的点P,使得以P,M,B为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)如图2,PM交线段BC于点Q,过点P作PE∥AC交x轴于点E,交线段BC于点F,请用含m的代数式表示线段QF的长,并求出当m为何值时QF有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴只有一个交点,以下四个结论:①抛物线的对称轴在
轴只有一个交点,以下四个结论:①抛物线的对称轴在![]() 轴左侧;②关于
轴左侧;②关于![]() 的方程
的方程![]() 有实数根;③
有实数根;③![]() ;④
;④![]() 的最大值为1.其中结论正确的为( )
的最大值为1.其中结论正确的为( )
A.①②③B.③④C.①③D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com