
分析 由a是方程x2+x-$\frac{1}{2}$=0的根知a2+a=$\frac{1}{2}$,将其代入到原式=$\frac{(a-1)({a}^{2}+a+1)}{({a}^{4}-{a}^{2})(a+1)}$=$\frac{(a-1)({a}^{2}+a+1)}{{a}^{2}(a+1)^{2}(a-1)}$=$\frac{{a}^{2}+a+1}{({a}^{2}+a)^{2}}$即可得.
解答 解:∵a是方程x2+x-$\frac{1}{2}$=0的根,
∴a2+a=$\frac{1}{2}$,
则原式=$\frac{(a-1)({a}^{2}+a+1)}{({a}^{4}-{a}^{2})(a+1)}$=$\frac{(a-1)({a}^{2}+a+1)}{{a}^{2}(a+1)^{2}(a-1)}$=$\frac{{a}^{2}+a+1}{({a}^{2}+a)^{2}}$=$\frac{1+\frac{1}{2}}{(\frac{1}{2})^{2}}$=6.
点评 本题主要考查一元二次方程的解,解题的关键是将原式变形成含有a2+a这样的整体,从而采用整体代入的办法求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
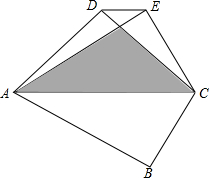 如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.
如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠EBC=32°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠EBC=32°,∠AEB=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com