
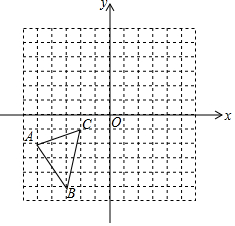
 在如图的直角坐标系中,每个小方格郡是边长为1的正方形,△ABC的顶点均在格点上点A的坐标(-5,-2).
在如图的直角坐标系中,每个小方格郡是边长为1的正方形,△ABC的顶点均在格点上点A的坐标(-5,-2).分析 (1)先写出B、C点的坐标,然后利用点平移的坐标规律写出A1、B1、C1的坐标,再描点即可;
(2)利用网格特点和旋转的性质画出点A2、B2、C2,从而得到△A2B2C2;
(3)先利用勾股定理计算出OA1、OB1,然后利用面积的和差和扇形的面积公式计算线段A1B1扫过的面积.
解答 解:(1)如图,△A1B1C1为所作,点B1的坐标为(3,-5);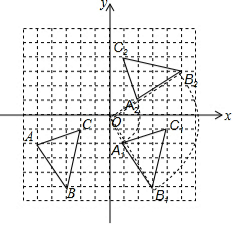
(2)如图,△A2B2C2为所作;
(3)OA1=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,OB1=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
所以旋转过程中线段A1B1扫过的面积=$\frac{90•π•(\sqrt{34})^{2}}{360}$-$\frac{90•π•(\sqrt{5})^{2}}{360}$=$\frac{29}{4}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:解答题
 如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
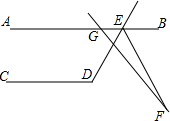 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )| A. | 10.5° | B. | 9.5° | C. | 8.5° | D. | 8° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
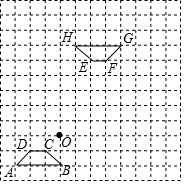 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD、四边形EFGH(顶点是网格线的交点)和格点O.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD、四边形EFGH(顶点是网格线的交点)和格点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
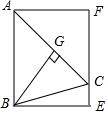 已知,△ABC中,AB=AC,∠BAC=45°,过C作CF∥AB,过A,B分别向直线CF作垂线,垂足分别为F,E,过B作BG⊥AC于G.
已知,△ABC中,AB=AC,∠BAC=45°,过C作CF∥AB,过A,B分别向直线CF作垂线,垂足分别为F,E,过B作BG⊥AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )| A. | (-3,1) | B. | (-2,2) | C. | (-3,3) | D. | (-3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
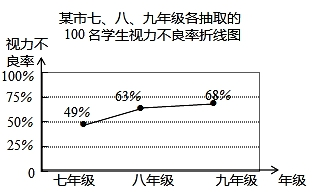
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
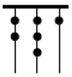 古时候,猎人通过结绳的方法来统计猎物的个数,如图,一位猎人在排列的绳子上从右到左依次打结,满八进一,用来记录一段时间内猎物的数量,由图可知,猎物的数量是153.
古时候,猎人通过结绳的方法来统计猎物的个数,如图,一位猎人在排列的绳子上从右到左依次打结,满八进一,用来记录一段时间内猎物的数量,由图可知,猎物的数量是153.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com