
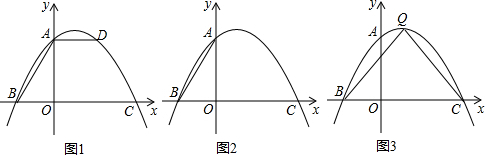
分析 (1)如图1,利用抛物线的对称性得到抛物线的对称轴为直线x=3,再判断点A与点D为抛物线上的对称点,于是可得AD的长;
(2)在Rt△ABO中,利用正弦定义计算出AB,利用勾股定理计算出OA,从而得到A点坐标,接着利用待定系数法求出抛物线解析式和直线AC的解析式,过点P作PM∥AC,如图2,利用直线PM与抛物线只有唯一公共点和判别式的意义可计算出m,于是得到此时P点和Q点坐标,然后根据三角形面积公式,利用S△PAC=S△PAQ+S△CPQ进行计算即可;
(3)如图3,作QH⊥BC于H,易得Q点的横坐标为3,△QBC为等腰三角形,当∠BQC=60°时,△BCQ为等边三角形,再求出Q点坐标,然后利用待定系数法求出抛物线解析式,从而得到A点坐标,易得此时t的值;当∠BQC=90°时,利用同样方法求t的值.
解答 解:(1)如图1,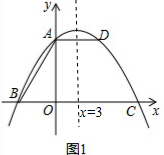
∵B(-2,0)和C(8,0)为抛物线上的对应点,
∴抛物线的对称轴为直线x=3,
∵AD∥x轴,
∴点A与点D为抛物线上的对称点,
∴AD=2×3=6;
(2)在Rt△ABO中,∵sin∠BAO=$\frac{BO}{AB}$=$\frac{\sqrt{5}}{5}$,
∴AB=$\sqrt{5}$OB=2$\sqrt{5}$,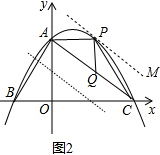
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-{2}^{2}}$=4,则A(0,4),
设抛物线解析式为y=a(x+2)(x-8),
把A(0,4)代入得a•2•(-8)=4,解得a=-$\frac{1}{4}$,
∴抛物线解析式为y=-$\frac{1}{4}$(x+2)(x-8),即y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
设直线AC的解析式为y=kx+b,
把A(0,4),C(8,0)代入得$\left\{\begin{array}{l}{b=4}\\{8k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直线AC的解析式为y=-$\frac{1}{2}$x+4,
过点P作PM∥AC,如图2,当直线PM与抛物线只有唯一公共点P时,此时对于△APC的面积所取的值,P点有且只有两个与之对应(两P点在AC的两侧,到AC的距离相等),作PQ∥y轴交AC于Q,
设直线PM的解析式为y=-$\frac{1}{2}$x+m,
则方程-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=-$\frac{1}{2}$x+m有两个相等的实数解,方程整理为x2-8x+4m-16=0,△=(-8)2-4×(4m-16)=0,解得m=8,解方程得x1=x2=4,此时P点坐标为(4,6),Q点坐标为(4,2)
S△PAC=S△PAQ+S△CPQ=$\frac{1}{2}$×(6-2)×8=16,
即△PAC的面积为16时,相应的P点有且只有两个;
(3)如图3,作QH⊥BC于H,
∵Q点为顶点,
∴Q点的横坐标为3,△QBC为等腰三角形,
当∠BQC=60°时,△BCQ为等边三角形,则QH=$\frac{\sqrt{3}}{2}$BC=5$\sqrt{3}$,
则Q(3,5$\sqrt{3}$),
设抛物线解析式为y=a(x+2)(x-8),
把Q(3,5$\sqrt{3}$)代入得a•5•(-5)=5$\sqrt{3}$,解得a=-$\frac{\sqrt{3}}{5}$,
∴抛物线解析式为y=-$\frac{\sqrt{3}}{5}$(x+2)(x-8),即y=-$\frac{\sqrt{3}}{5}$x2+$\frac{6\sqrt{3}}{5}$x+$\frac{16\sqrt{3}}{5}$,
当x=0时,y=-$\frac{\sqrt{3}}{5}$x2+$\frac{6\sqrt{3}}{5}$x+$\frac{16\sqrt{3}}{5}$=$\frac{16\sqrt{3}}{5}$,则A(0,$\frac{16\sqrt{3}}{5}$),此时t的值为$\frac{16\sqrt{3}}{5}$,
当∠BQC=90°时,△BCQ为等腰直角三角形,则QH=$\frac{1}{2}$BC=5,
则Q(3,5),
设抛物线解析式为y=a(x+2)(x-8),
把Q(3,5)代入得a•5•(-5)=5,解得a=-$\frac{1}{5}$,
∴抛物线解析式为y=-$\frac{1}{5}$(x+2)(x-8),即y=-$\frac{1}{5}$x2+$\frac{6}{5}$x+$\frac{16}{5}$,
当x=0时,y=-$\frac{1}{5}$x2+$\frac{6}{5}$x+$\frac{16}{5}$=$\frac{16}{5}$,则A(0,$\frac{16}{5}$),此时t的值为$\frac{16}{5}$,
∴当60°≤∠BQC≤90°时,t取值范围为$\frac{16}{5}$≤t≤$\frac{16\sqrt{3}}{5}$.
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等边三角形的性质和等腰直角三角形的性质;会利用待定系数法求二次函数和一次函数解析式;会利用判别式判断直线与抛物线的交点个数;理解坐标与图形性质,记住三角形面积公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解2016年春节联欢晚会收视情况,应采用全面调查方式 | |
| B. | 为了解全国中学生的视力状况,应采用普查方式 | |
| C. | 乘坐高铁时,检查旅客行李是否携带有违禁物品应采用抽样调查方式 | |
| D. | 为了解2016年春节中国人最喜欢的过年方式应采用抽样调查方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
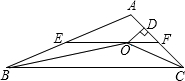 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①∠BOC=90°+$\frac{1}{2}∠A$;②EF=BE+CF;③设OD=m,AE:AF=n,则S△AEF=$\frac{1}{2}mn$;④EF是△ABC的中位线.其中正确的结论是 ( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①∠BOC=90°+$\frac{1}{2}∠A$;②EF=BE+CF;③设OD=m,AE:AF=n,则S△AEF=$\frac{1}{2}mn$;④EF是△ABC的中位线.其中正确的结论是 ( )| A. | ②③ | B. | ②③④ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
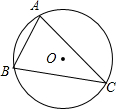 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
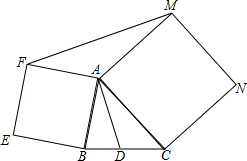 已知:如图,分别以△ABC的边AB、AC为边长向△ABC外作正方形ABEF和正方形ACNM,点D是BC的中点,连接AD、FM.
已知:如图,分别以△ABC的边AB、AC为边长向△ABC外作正方形ABEF和正方形ACNM,点D是BC的中点,连接AD、FM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
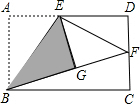 如图,在长方形ABCD中,AB=3,BC=2$\sqrt{6}$,点E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.
如图,在长方形ABCD中,AB=3,BC=2$\sqrt{6}$,点E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com