
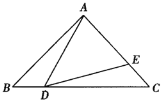
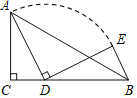
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=1.点D在BC边上(不与B,C点重合),作∠ADE=45°,DE与AC交于点E.
(1)求证:△ABD ∽△DCE;
(2)设BD=x,请用含x的代数式表示AE;
(3)当BD=1时,求△ADE的面积.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据等腰直角三角形的性质及三角形内角与外角的关系,易证△ABD∽△DCE.
(2)由△ABD∽△DCE,对应边成比例及等腰直角三角形的性质可求答案;
(3)作DF⊥AC,证得△DFC ∽△BAC,利用对应边成比例求得DF,再根据(2)的结论结合三角形面积公式即可求得答案.
(1)∵在△ABC中,∠BAC=90°,AB=AC
∴∠B=∠C=45°
∵∠CDA=∠BAD+∠B=∠CDE+∠ADE,∠ADE=∠B=45°,
∴∠BAD=∠CDE,
∴△ABD ∽△DCE;
(2)在△ABC中,∠BAC=90°,AB=AC=1,
∴BC=![]() ,
,![]() ,
,
∵△ABD ∽△DCE,BD=x,
∴![]() ,即
,即![]() ,
,
![]() ,
,
![]() ;
;
(3)∵BD![]() ,AB=AC=1,BC=
,AB=AC=1,BC=![]() ,CD
,CD![]() ,
,
由(2)得![]() ,
,
过点D作DF⊥AC,垂足为F,如图,
∠DFC=90°,
∵∠BAC=90°,
∴DF∥AB,

∴△DFC ∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
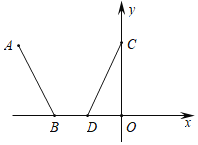
【题目】如图,已知A(﹣6,4),B(﹣4,0),将线段AB沿直线x=﹣3进行轴对称变换得到对应线段CD.
(1)直接写出C点的坐标为 ,D点的坐标为 ;
(2)将线段CD绕O点旋转180°得对应线段EF,请你画出线段EF;
(3)将线段EF沿y轴正方向平移m个单位,当m= 时,线段EF与CD成轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,B,C,D三点在![]() 上,
上,![]() ,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
,PA是钝角△ABC的高线,PA的延长线与线段CD交于点E.
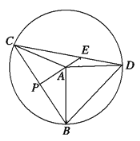
(1)请在图中找出一个与∠CAP相等的角,这个角是 ;
(2)用等式表示线段AC,EC,ED之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
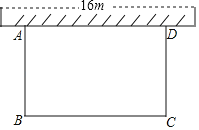
【题目】某居民小区要在一块一边靠墙的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为32m的栅栏围成(如图所示).如果墙长16m,满足条件的花园面积能达到120m2吗?若能,求出此时BC的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACD中,∠ACD=90°,AC=b,CD=a,AD=c,点B在CD的延长线上
(1)求证:关于x的一元二次方程![]() 必有实数根
必有实数根
(2)当b=3,CB=5时.将线段AD绕点D顺时针旋转90°,得到线段DE,连接BE,则当a的值为多少时,线段BE的长最短,最短长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com