
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y= ![]() x2+2x与x轴相交于O、B,顶点为A,连接OA.
x2+2x与x轴相交于O、B,顶点为A,连接OA.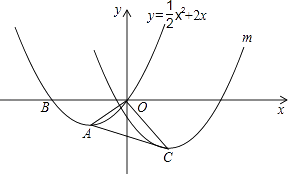
(1)求点A的坐标和∠AOB的度数;
(2)若将抛物线y= ![]() x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
x2+2x向右平移4个单位,再向下平移2个单位,得到抛物线m,其顶点为点C.连接OC和AC,把△AOC沿OA翻折得到四边形ACOC′.试判断其形状,并说明理由;
(3)在(2)的情况下,判断点C′是否在抛物线y= ![]() x2+2x上,请说明理由.
x2+2x上,请说明理由.
(4)若点P为x轴上的一个动点,试探究在抛物线m上是否存在点Q,使以点O、P、C、Q为顶点的四边形是平行四边形,且OC为该四边形的一条边?若存在,请直接写出点Q的坐标;若不存在,请说明理由. (参考公式:二次函数y=ax2+bx+c(a≠0)图象的顶点坐标为( ![]() ,
, ![]() ),对称轴是直线x=
),对称轴是直线x= ![]() .)
.)
【答案】
(1)
解:∵由y= ![]() x2+2x得,y=
x2+2x得,y= ![]() (x+2)2﹣2,
(x+2)2﹣2,
∴抛物线的顶点A的坐标为(﹣2,﹣2),
令 ![]() x2+2x=0,解得x1=0,x2=﹣4,
x2+2x=0,解得x1=0,x2=﹣4,
∴点B的坐标为(﹣4,0),
过点A作AD⊥x轴,垂足为D,
∴∠ADO=90°,
∴点A的坐标为(﹣2,﹣2),点D的坐标为(﹣2,0),
∴OD=AD=2,
∴∠AOB=45°;
(2)
解:四边形ACOC′为菱形.
由题意可知抛物线m的二次项系数为 ![]() ,且过顶点C的坐标是(2,﹣4),
,且过顶点C的坐标是(2,﹣4),
∴抛物线的解析式为:y= ![]() (x﹣2)2﹣4,即y=
(x﹣2)2﹣4,即y= ![]() x2﹣2x﹣2,
x2﹣2x﹣2,
过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,
∴OE=2,CE=4,AF=4,CF=CE﹣EF=2,
∴OC= ![]() =2
=2 ![]() ,
,
同理,AC=2 ![]() ,OC=AC,
,OC=AC,
由翻折不变性的性质可知,OC=AC=OC′=AC′,
故四边形ACOC′为菱形.
(3)
解:如图1,点C′不在抛物线y= ![]() x2+2x上.
x2+2x上.

理由如下:
过点C′作C′G⊥x轴,垂足为G,
∵OC和OC′关于OA对称,∠AOB=∠AOH=45°,
∴∠COH=∠C′OG,
∵CE∥OH,
∴∠OCE=∠C′OG,
又∵∠CEO=∠C′GO=90°,OC=OC′,
∴△CEO≌△C′GO,
∴OG=CE=4,C′G=OE=2,
∴点C′的坐标为(﹣4,2),
把x=﹣4代入抛物线y= ![]() x2+2x得y=0,
x2+2x得y=0,
∴点C′不在抛物线y= ![]() x2+2x上;
x2+2x上;
(4)
解:

存在符合条件的点Q.
∵点P为x轴上的一个动点,点Q在抛物线m上,
∴设Q(a, ![]() (a﹣2)2﹣4),
(a﹣2)2﹣4),
∵OC为该四边形的一条边,
∴OP为对角线,
∴ ![]() =0,解得a1=6,a2=﹣2(舍去),
=0,解得a1=6,a2=﹣2(舍去),
∴点Q的坐标为(6,4).
【解析】(1)由y= ![]() x2+2x得,y=
x2+2x得,y= ![]() (x+2)2﹣2,故可得出抛物线的顶点A的坐标,令
(x+2)2﹣2,故可得出抛物线的顶点A的坐标,令 ![]() x2+2x=0得出点B的坐标过点A作AD⊥x轴,垂足为D,由∠ADO=90°可知点D的坐标,故可得出OD=AD,由此即可得出结论;(2)由题意可知抛物线m的二次项系数为
x2+2x=0得出点B的坐标过点A作AD⊥x轴,垂足为D,由∠ADO=90°可知点D的坐标,故可得出OD=AD,由此即可得出结论;(2)由题意可知抛物线m的二次项系数为 ![]() ,由此可得抛物线m的解析式过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,根据勾股定理可求出OC的长,同理可得AC的长,OC=AC,由翻折不变性的性质可知,OC=AC=OC′=AC′,由此即可得出结论;(3)过点C′作C′G⊥x轴,垂足为G,由于OC和OC′关于OA对称,∠AOB=∠AOH=45°,故可得出∠COH=∠C′OG,再根据CE∥OH可知∠OCE=∠C′OG,根据全等三角形的判定定理可知△CEO≌△C′GO,故可得出点C′的坐标把x=﹣4代入抛物线y=
,由此可得抛物线m的解析式过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,根据勾股定理可求出OC的长,同理可得AC的长,OC=AC,由翻折不变性的性质可知,OC=AC=OC′=AC′,由此即可得出结论;(3)过点C′作C′G⊥x轴,垂足为G,由于OC和OC′关于OA对称,∠AOB=∠AOH=45°,故可得出∠COH=∠C′OG,再根据CE∥OH可知∠OCE=∠C′OG,根据全等三角形的判定定理可知△CEO≌△C′GO,故可得出点C′的坐标把x=﹣4代入抛物线y= ![]() x2+2x进行检验即可得出结论;(4)由于点P为x轴上的一个动点,点Q在抛物线m上,故设Q(a,
x2+2x进行检验即可得出结论;(4)由于点P为x轴上的一个动点,点Q在抛物线m上,故设Q(a, ![]() (a﹣2)2﹣4),由于OC为该四边形的一条边,故OP为对角线,由于点P在x轴上,根据中点坐标的定义即可得出a的值,故可得出结论.
(a﹣2)2﹣4),由于OC为该四边形的一条边,故OP为对角线,由于点P在x轴上,根据中点坐标的定义即可得出a的值,故可得出结论.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2= ![]() (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n)
(m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n) 
(1)求反比例函数与一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)直接写出当y1<y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题: 
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
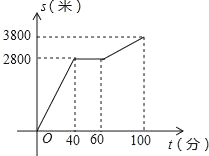
A. 小明中途休息用了20分钟
B. 小明休息前爬山的平均速度大于休息后爬山的平均速度
C. 小明在上述过程中所走的路程为6600米
D. 小明休息前爬山的平均速度为每分钟70米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点B(a,5)在第二象限,点C在y轴上移动,以BC为斜边作等腰直角△BCD,我们发现直角顶点D点随着C点的移动也在一条直线上移动,这条直线的函数表达式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.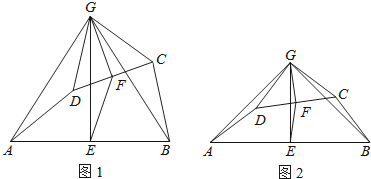
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2 , 若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
为奇数的正整数);并且运算重复进行.例如,取n=26,第3次“F运算”的结果是11.则:若n=449,则第449次“F运算”的结果是____.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com