
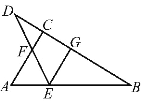
【题目】如图,在Rt△ABC中,∠ACB=90°,D是BC延长线上的一点,线段BD的垂直平分线EG交AB于点E,交BD于点G.
(1)当∠B=30°时,AE和EF有什么关系?请说明理由.
(2)当点D在BC的延长线上(CD<BC)运动时,点E是否在线段AF的垂直平分线上?
【答案】(1)AE=EF(2)点E是在线段AF的垂直平分线上
【解析】
(1)根据线段垂直平分线性质得出DE=BE,求出∠D=∠B=30°,根据三角形内角和定理和三角形外角性质求出∠A=∠DEA=60°,即可得出答案.
(2)求出∠A=∠AFE,根据线段垂直平分线性质得出即可.
解:
(1)AE=EF.理由如下:
∵线段BD的垂直平分线EG交AB于点E,交BD于点G,
∴DE=BE,
∵∠B=30°,
∴∠D=∠B=30°,
∴∠DEA=∠D+∠B=60°,
∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=∠DEA=60°,
∴△AEF是等边三角形,
∴AE=EF.
(2)点E是在线段AF的垂直平分线上.理由如下:
∵∠B=∠D,∠ACB=90°=∠FCD,
∴∠A=∠DFC,
∵∠DFC=∠AFE,
∴∠A=∠AFE,
∴EF=AE,
∴点E在线段AF的垂直平分线上.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
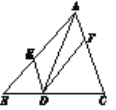
【题目】如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.则下列说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中正确的是______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )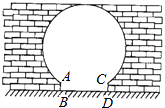
A.2米
B.2.5米
C.2.4米
D.2.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用完全平方公式进行因式分解,解答下列问题:
![]() 因式分解:
因式分解:![]() .
.
![]() 填空: ①当
填空: ①当![]() 时,代数式
时,代数式![]() _ .
_ .
②当![]() _ 时,代数式
_ 时,代数式![]() .
.
③代数式![]() 的最小值是_ .
的最小值是_ .
![]() 拓展与应用:求代数式
拓展与应用:求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=2,AD=3,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A′EF,则A′C的长的最小值是 . 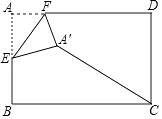
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )
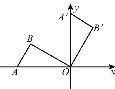
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com