
【题目】如图是一个“有理数转换器”(箭头是指有理数进入转换器后的路径,方框是对进入的数进行转换的转换器)
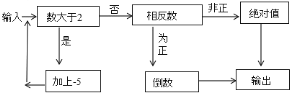
![]() 当小明输入
当小明输入![]() ;
;![]() ;
;![]() 这三个数时,这三次输入的结果分别是多少?
这三个数时,这三次输入的结果分别是多少?
![]() 你认为当输入什么数时,其输出的结果是
你认为当输入什么数时,其输出的结果是![]() ?
?
![]() 你认为这的“有理数转换器”不可能输出什么数?
你认为这的“有理数转换器”不可能输出什么数?
【答案】(1)当输入![]() 时,输出
时,输出![]() ;当输入
;当输入![]() 时,输出
时,输出![]() ;当输入
;当输入![]() 时,输出
时,输出![]() (2)应输入
(2)应输入![]() 或
或![]() (
(![]() 为自然数);(3)输出的数应为非负数
为自然数);(3)输出的数应为非负数
【解析】
(1)先判断出3、![]() 、0.4与2的大小,再根据所给程序图找出合适的程序进行计算即可;
、0.4与2的大小,再根据所给程序图找出合适的程序进行计算即可;
(2)由此程序可知,当输出0时,因为0的相反数及绝对值均为0,所以应输入0;
(3)根据绝对值的性质和倒数的定义可找出规律.
解:![]() ∵
∵![]() ,
,
∴输入![]() 时的程序为:
时的程序为:![]() ,
,
∴![]() 的相反数是
的相反数是![]() ,
,![]() 的倒数是
的倒数是![]() ,
,
∴当输入![]() 时,输出
时,输出![]() ;
;
∵![]() .
.
∴输入![]() 时的程序为:
时的程序为:![]() ,
,
∴![]() 的相反数是
的相反数是![]() ,
,![]() ,
,
∴当输入![]() 时,输出
时,输出![]() ;
;
∵![]() ,
,
∴输入![]() 时的程序为:
时的程序为:![]() ,
,![]() 的相反数为
的相反数为![]() ,
,![]() 的绝对值是
的绝对值是![]()
∴当输入![]() 时,输出
时,输出![]() .
.
![]() ∵输出数为
∵输出数为![]() ,
,![]() 的相反数及绝对值均为
的相反数及绝对值均为![]() ,当输入
,当输入![]() 的倍数时也输出
的倍数时也输出![]() .
.
∴应输入![]() 或
或![]() (
(![]() 为自然数);
为自然数);
![]() 由图表知,不管输入正数、
由图表知,不管输入正数、![]() 或者负数,输出的结果都是非负数.
或者负数,输出的结果都是非负数.
所以输出的数应为非负数.


科目:初中数学 来源: 题型:
【题目】如图,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),求该光盘的直径是多少? 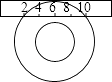
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加![]() 场比赛,其中
场比赛,其中![]() 分球的命中率为
分球的命中率为![]() ,平均每场有
,平均每场有![]() 次
次![]() 分球未投中.
分球未投中.
![]() 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个![]() 分球?
分球?
![]() 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员![]() 分球共出手
分球共出手![]() 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了![]() 个
个![]() 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80分钟通话时间,超过80分钟的部分,以每分钟0.15元的价格计费.
下列结论:
①如图描述的是方式1的收费方法;
②若月通话时间少于240分钟,选择方式2省钱;
③若月通讯费为50元,则方式1比方式2的通话时间多;
④若方式1比方式2的通讯费多10元,则方式1比方式2的通话时间多100分钟.
其中正确的是( )
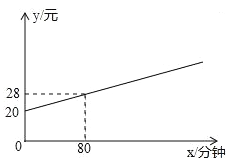
A.只有①② B.只有③④ C.只有①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数关系的图像.
(1)他们出发半小时后,离家多少千米?
(2)求出AB段的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面相同的纸牌A,B,C,D,其正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色.小明将这4张纸牌背面朝上洗匀后,摸出一张,将剩余3张洗匀后再摸出一张.请用画树状图或列表的方法求摸出的两张牌均为黑色的概率. 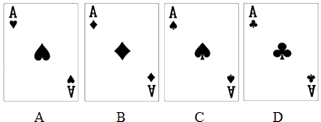
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是_____(填写符合要求的序号)
(1)两个有理数的和为负数时,这两个数都是负数;
(2)如果两个数的差是正数,那么这两个数都是正数;
(3)几个有理数相乘,当负因数个数为奇数时,乘积一定为负;
(4)数轴上到原点的距离为3的点表示的数是3或﹣3;
(5)0乘以任何数都是0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家高斯在上学时曾经研究过这样一个问题,![]() ?
?
经过研究,这个问题的一般性结论是![]() ,其中
,其中![]() 为正整数,现在我们来研究一个类似的问题:
为正整数,现在我们来研究一个类似的问题:![]() ?
?
观察下面三个特殊的等式:
![]()
![]()
![]()
将这三个等式的两边相加,可以得到![]() .
.
读完这段材料,请你计算:
(1)![]() ________;(直接写出结果)
________;(直接写出结果)
(2)![]() ;(写出计算过程)
;(写出计算过程)
(3)![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com