
【题目】“五一”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数关系的图像.
(1)他们出发半小时后,离家多少千米?
(2)求出AB段的函数表达式.

【答案】(1)他们出发半小时后,离家30千米;(2) y=80x-30(1.5≤x≤2.5).
【解析】(1)先运用待定系数法求出OA的解析式,再将x=0.5代入,求出y的值即可;
(2)设AB段图象的函数表达式为y=k′x+b,将A、B两点的坐标代入,运用待定系数法即可求解;
(1)设OA段的函数表达式为y=kx.
∵当x=1.5时,y=90,∴1.5k=90,∴k=60,
∴y=60x(0≤x≤1.5).
当x=0.5时,y=60×0.5=30,
故他们出发半小时后,离家30千米.
(2)设AB段的函数表达式为y=k′x+b.
把点A(1.5,90),点B(2.5,170)代入得![]() ;解得
;解得![]() ,
,
∴y=80x-30(1.5≤x≤2.5).


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线AB:y=5x﹣5与x轴交于点A,与y轴交于点B,点C与点B关于原点O对称,抛物线y=ax2+bx+c的对称轴为直线x=3且过点A和C. 
(1)求点A和点C的坐标;
(2)求抛物线y=ax2+bx+c的解析式;
(3)若抛物线y=ax2+bx+c的顶点为D,且在x轴上存在点P使得△DAP的面积为6,直接写出满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个“有理数转换器”(箭头是指有理数进入转换器后的路径,方框是对进入的数进行转换的转换器)
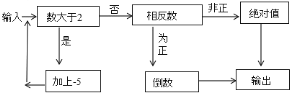
![]() 当小明输入
当小明输入![]() ;
;![]() ;
;![]() 这三个数时,这三次输入的结果分别是多少?
这三个数时,这三次输入的结果分别是多少?
![]() 你认为当输入什么数时,其输出的结果是
你认为当输入什么数时,其输出的结果是![]() ?
?
![]() 你认为这的“有理数转换器”不可能输出什么数?
你认为这的“有理数转换器”不可能输出什么数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石头剪子布,又称“猜丁壳”,是一种起源于中国流传多年的猜拳游戏.游戏时的各方每次用一只手做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”.两人游戏时,若出现相同手势,则不分胜负游戏继续,直到分出胜负,游戏结束.三人游戏时,若三种手势都相同或都不相同,则不分胜负游戏继续;若出现两人手势相同,则视为一种手势与第三人所出手势进行对决,此时,参照两人游戏规则.例如甲、乙二人同时出石头,丙出剪刀,则甲、乙获胜.假定甲、乙、丙三人每次都是随机地做这三种手势,那么:
(1)请你用画树状图或列表的方式,求出一次游戏中甲、乙两人出第一次手势时,不分胜负的概率;
(2)请直接写出一次游戏中甲、乙、丙三人出第一次手势时,不分胜负的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
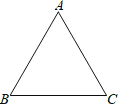
【题目】如图,在等边三角形ABC中,AB=5,在AB边上有一点P,过点P作PM⊥BC,垂足为M,过点M作MN⊥AC,垂足为N,过点N作NQ⊥AB,垂足为Q.当PQ=1时,BP=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com